Twenty-five adults reported the amount of time each spent exercising during a particular week. The results are summarized in the...
GMAT Graphics Interpretation : (GI) Questions
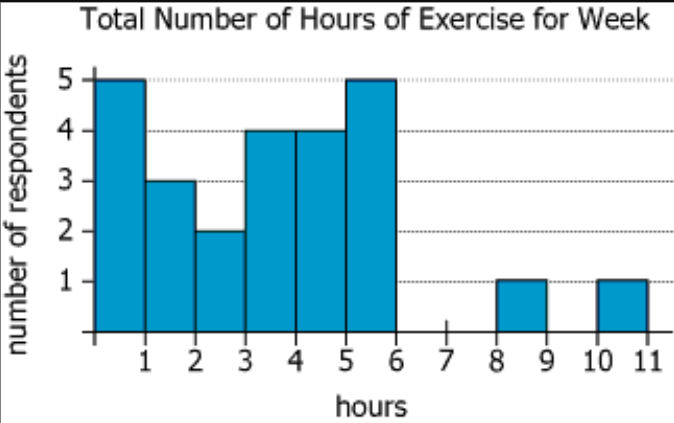
Twenty-five adults reported the amount of time each spent exercising during a particular week. The results are summarized in the graph as follows: 5 respondents reported exercising for less than 1 hour, 3 respondents reported exercising for at least 1 hour but less than 2, and so on.
Based on the given information, use the drop-down menus to most accurately complete the following statements.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Study participants | Twenty-five adults reported the amount of time each spent exercising during a particular week | 25 adults tracked their total weekly exercise time |
| Data presentation introduction | The results are summarized in the graph as follows: | A summary of responses is shown visually |
| First interval example | 5 respondents reported exercising for less than 1 hour | 5 people exercised between 0 and 1 hour in the week |
| Second interval example | 3 respondents reported exercising for at least 1 hour but less than 2 | 3 people exercised between 1 and 2 hours in the week |
| Continuation phrase | and so on | The same structure applies to following hour intervals and their counts |
Table 2: Chart Analysis
| Chart Component | What's Shown | Meaning |
|---|---|---|
| Chart type | Histogram with bars representing numbers of respondents per hour interval | Displays how many people fall into each 1-hour exercise range |
| X-axis | Hours (intervals from 0-1, 1-2, ..., up to 10-11) | Groups weekly exercise time into ranges |
| Y-axis | Number of respondents (marked from 0 to 5) | The count of people in each range (maximum per bar is 5) |
| Main clusters | Two peaks: 0-1 hours (5 people), 5-6 hours (5 people) | Most exercise either very little or moderately (5-6 hours/week) |
| Gaps in data | 0 respondents for 6-7 and 7-8 hours | No one exercises between 6 and 8 hours/week; a distinct separation in exercise habits |
| Outliers | 1 person each at 8-9 and 10-11 hours | Only two people report unusually high weekly exercise |
Key Insights
The dataset shows a clear split in exercise behavior. The majority of respondents (\(\frac{23}{25}\)) exercise between 0 and 6 hours per week, concentrated at the low (0-1 hours) and moderate (5-6 hours) ends, creating a bimodal pattern. Two participants report much higher exercise (8-9 hours and 10-11 hours), with an empty gap in the 6-8 hour range. This suggests most people are either low or moderate exercisers, with very few high exercisers and no 'in-between' cases. The minimum possible average is about 3.1 hours per week, but many respondents exercise less than 3 hours. The data highlights both a tendency toward minimal activity and a smaller group of regular exercisers, but a near total absence of people in the 6-8 hour range.
Step-by-Step Solution
Question 1: Finding the Minimum Possible Mean of Weekly Exercise Hours
Complete Statement:
The least possible value for the mean of the numbers of hours of exercise reported for the week is [BLANK].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: least possible value
- Meaning: We are looking for the smallest possible mean based on the provided data.
- Relation to Chart: We must use the lower boundaries of each interval for each respondent to minimize the total sum.
- Important Implications: Assuming every respondent exercised only the minimum number of hours within their interval leads to the least possible mean.
- Key Phrase: least possible value
- Statement Breakdown 2:
- Key Phrase: mean of the numbers of hours
- Meaning: The average number of hours exercised per respondent in one week.
- Relation to Chart: We need to sum all assumed values and divide by the total respondents (25).
- Important Implications: Mean = (total minimum possible hours) / (number of respondents).
- Key Phrase: mean of the numbers of hours
- What is needed: The absolute minimum average (mean) number of hours per week based on the histogram data.
Solution:
- Condensed Solution Implementation:
Assume every respondent is at the minimum value in their indicated interval, sum these minimums, and divide by the total respondents (25) for the mean. - Necessary Data points:
Number of respondents per interval: 0–1 (5), 1–2 (3), 2–3 (2), 3–4 (4), 4–5 (4), 5–6 (5), 8–9 (1), 10–11 (1). Ignore empty intervals.- Calculations Estimations:
Total minimum hours: \((5\times0) + (3\times1) + (2\times2) + (4\times3) + (4\times4) + (5\times5) + (1\times8) + (1\times10) = 0 + 3 + 4 + 12 + 16 + 25 + 8 + 10 = 78\) hours. Divide by 25: \(\frac{78}{25} = 3.12\) hours. - Comparison to Answer Choices:
The answer choices include: 3, 3.12, 3.48, 3.98. The calculation matches 3.12.
- Calculations Estimations:
FINAL ANSWER Blank 1: 3.12
Question 2: Determining How Many Exceeded Less Than Half-Hour Daily Average
Complete Statement:
The number of respondents who exercised on average less than one-half hour per day during the week is between [BLANK], inclusive.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: exercised on average less than one-half hour per day
- Meaning: Respondents who, when dividing their weekly total by 7, average less than 0.5 hours per day.
- Relation to Chart: \(0.5 \times 7 = 3.5\) hours/week; so look for those below 3.5 hours/week.
- Key Phrase: exercised on average less than one-half hour per day
- Statement Breakdown 2:
- Key Phrase: number of respondents
- Meaning: How many people meet this criterion.
- Relation to Chart: Sum the number in each interval meeting the condition.
- Key Phrase: number of respondents
- What is needed: Minimum and maximum number of respondents with less than 3.5 hours exercise per week.
Solution:
- Condensed Solution Implementation:
Count definitely qualifying intervals, and account for any overlap in intervals that straddle the boundary for the range. - Necessary Data points:
Intervals: 0–1 (5), 1–2 (3), 2–3 (2) are all under 3.5 hours. 3–4 (4) includes part below and part above 3.5.- Calculations Estimations:
Minimum: Only those in 0–3 intervals (5+3+2) = 10. Maximum: Assume all 4 people in 3–4 are below 3.5, 10+4=14. - Comparison to Answer Choices:
Choices include: 0 and 5, 5 and 8, 8 and 10, 10 and 14, 14 and 19. The correct range is 10 and 14.
- Calculations Estimations:
FINAL ANSWER Blank 2: 10 and 14
Summary
To minimize the mean weekly exercise hours, assume each respondent is at the lower bound of their interval. This results in a minimum possible mean of 3.12 hours. For the number of respondents averaging less than 0.5 hours daily (3.5 per week), a certain 10 and as many as 14 could qualify, so the range is 10 and 14.
Question Independence Analysis
The two questions are independent: the mean (question 1) involves summing minimum possible values across all respondents, while the count (question 2) involves determining a range of qualifying individuals. Solving one does not require information from the other.