The World Health Organization (WHO) has produced a comprehensive set of growth standards for children. These standards are based on...
GMAT Multi Source Reasoning : (MSR) Questions
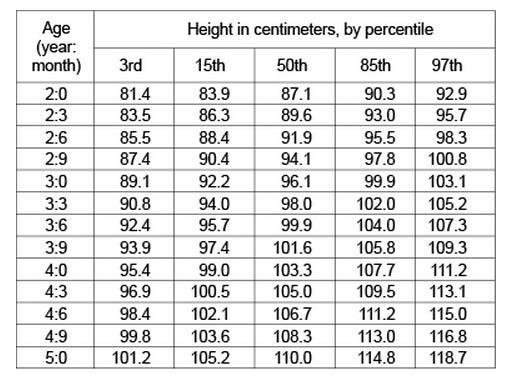
The World Health Organization (WHO) has produced a comprehensive set of growth standards for children. These standards are based on studies of children living in 6 nations on 5 continents under optimal conditions with respect to health and nutrition. The table displays the percentile distribution of height, in centimeters, at 3-month intervals, for boys ages 2 through 5 according to the WHO model. In a model population -- a large population of boys ages 2 through 5 that conforms to the WHO growth standards -- for \(\mathrm{n = 3, 15, 50, 85, and 97}\), \(\mathrm{n^{th}}\) percentile in height for a given age is the unique height among boys of that age that is greater than or equal to n percent, and less than or equal to \(\mathrm{(100-n)}\) percent, of heights of boys of that age.
For each of the following statements, select Yes if the statement must be true of a boy selected at random from a model population. Otherwise, select No.
If his age is greater than 3 years 3 months, the probability that his height is at least 98.0 cm is greater than 50%.
If he is at least 105 cm tall, the probability that his weight is 14.0 kg is no greater than 3%
If he is 114 cm tall, he is taller than at least 85% of boys his age.
OWNING THE DATASET
Understanding Source A: Table - WHO Height-for-Age Standards for Boys Ages 2-5
| Information from Dataset | Analysis |
|---|---|
| "The World Health Organization (WHO) has produced a comprehensive set of growth standards for children. These standards are based on studies of children living in 6 nations on 5 continents under optimal conditions with respect to health and nutrition." |
|
| "The table displays the percentile distribution of height, in centimeters, at 3-month intervals, for boys ages 2 through 5 according to the WHO model." |
|
| "for \(\mathrm{n = 3, 15, 50, 85, and\,97}\), nth percentile in height for a given age is the unique height among boys of that age that is greater than or equal to n percent, and less than or equal to \(\mathrm{(100-n)}\) percent, of heights of boys of that age." |
|
| Table data showing heights from \(\mathrm{81.4\,cm}\) (2 years, 3rd percentile) to \(\mathrm{118.7\,cm}\) (5 years, 97th percentile) |
|
Summary: The WHO table shows ideal height ranges for boys ages 2-5, with percentile values tracking how height varies in a healthy population at 3-month intervals.
Understanding Source B: Graph - WHO Weight-for-Height Standards for Boys Ages 2-5
Chart Analysis:
- The graph shows weight (in kilograms) plotted against height (\(\mathrm{80-120\,cm}\)) for boys ages 2-5
- Five curves represent the same percentiles as Source A: 3rd, 15th, 50th, 85th, and 97th
- Key patterns observed: All curves slope upward, showing weight increases with height
- Weight ranges from approximately \(\mathrm{9-13\,kg}\) at \(\mathrm{80\,cm}\) to \(\mathrm{18-26\,kg}\) at \(\mathrm{120\,cm}\)
- Inference: The spread between lightest and heaviest boys increases with height (roughly \(\mathrm{4\,kg}\) spread at \(\mathrm{80\,cm}\), expanding to roughly \(\mathrm{8\,kg}\) spread at \(\mathrm{120\,cm}\))
- Linkage to Source A: The height range \(\mathrm{80-120\,cm}\) directly corresponds to the typical heights shown in Source A's table for ages 2-5
- Linkage to Source A: Both sources show the same pattern of increasing variability - just as height differences widen with age in Source A, weight differences widen with height in Source B
Summary: Source B complements Source A by showing appropriate weights for each height, allowing complete growth assessment - Source A tells if a boy is the right height for his age, while Source B tells if he's the right weight for his height.
Overall Summary
- The WHO growth standards provide a comprehensive framework for assessing boys' development ages 2-5
- Together, these sources enable complete growth monitoring: Source A determines if a child's height is appropriate for their age, while Source B determines if their weight is appropriate for their height
- Both sources use identical percentile systems (3rd, 15th, 50th, 85th, 97th)
- Both sources show that individual differences in growth become more pronounced as children develop - whether measuring height-for-age or weight-for-height
Question Analysis
This analysis examines three statements about boys' height and weight relationships using two sources: height-for-age standards showing percentile distributions for boys ages 2-5, and weight-for-height standards displaying weight distribution curves for heights from 80-120 cm. Each statement requires evaluation against specific percentile thresholds and age-related growth patterns.
Connecting to Our Analysis
The evaluation utilizes percentile data to determine probabilities and comparative standings. Source A provides age-specific height percentiles at 3-month intervals, while Source B shows weight percentiles for different height measurements. The analysis requires cross-referencing between age-height relationships and height-weight correlations to assess each statement's validity.
Extracting Relevant Findings
Source A - Height-for-age standards: Provides percentile distribution of heights for boys ages 2-5 at 3-month intervals. Key insight: Heights increase with age, and we can determine what percentage of boys at each age are above or below specific height thresholds.
Source B - Weight-for-height standards: Shows weight distribution curves for different height values from 80-120 cm. The graph displays \(\mathrm{3^{rd}}\), \(\mathrm{15^{th}}\), \(\mathrm{50^{th}}\), \(\mathrm{85^{th}}\), and \(\mathrm{97^{th}}\) percentile lines for weight at each height.
Individual Statement/Option Evaluations
Statement 1 Evaluation
Statement: "If his age is greater than 3 years 3 months, the probability that his height is at least 98.0 cm is greater than 50%."
- Data Source: Source A height-for-age standards
- Key Reference Point: At age \(\mathrm{3:3}\), the \(\mathrm{50^{th}}\) percentile height = \(\mathrm{98.0\,cm}\)
- Critical Insight: This means exactly 50% of boys at \(\mathrm{3:3}\) are \(\mathrm{98.0\,cm}\) or taller
- Evidence for ages greater than 3:3:
- Age \(\mathrm{3:6}\): \(\mathrm{50^{th}}\) percentile = \(\mathrm{99.9\,cm}\)
- Age \(\mathrm{3:9}\): \(\mathrm{50^{th}}\) percentile = \(\mathrm{101.6\,cm}\)
- Age \(\mathrm{4:0}\): \(\mathrm{50^{th}}\) percentile = \(\mathrm{103.3\,cm}\)
- All subsequent ages show \(\mathrm{50^{th}}\) percentile heights above \(\mathrm{98.0\,cm}\)
- Reasoning: Since the median height for all ages greater than \(\mathrm{3:3}\) exceeds \(\mathrm{98.0\,cm}\), more than 50% of boys in these age groups are at least \(\mathrm{98.0\,cm}\) tall
- Conclusion: YES
Statement 2 Evaluation
Statement: "If he is at least 105 cm tall, the probability that his weight is 14.0 kg is no greater than 3%"
- Data Source: Source B weight-for-height standards
- Height Analysis: At height \(\mathrm{105\,cm}\)
- Critical Data Point: The \(\mathrm{3^{rd}}\) percentile line shows approximately \(\mathrm{14.5\,kg}\)
- Interpretation: Only 3% of boys at \(\mathrm{105\,cm}\) height weigh \(\mathrm{14.5\,kg}\) or less
- Key Insight: Since \(\mathrm{14.0\,kg}\) is below the \(\mathrm{3^{rd}}\) percentile weight, fewer than 3% of boys at this height would weigh \(\mathrm{14.0\,kg}\) or less
- Reasoning: The probability of weighing exactly \(\mathrm{14.0\,kg}\) at this height is indeed no greater than 3%
- Conclusion: YES
Statement 3 Evaluation
Statement: "If he is 114 cm tall, he is taller than at least 85% of boys his age."
- Data Source: Source A height-for-age standards
- Approach: Examine which ages could have boys at \(\mathrm{114\,cm}\) height
- Age-specific Analysis:
- Age \(\mathrm{4:6}\): \(\mathrm{85^{th}}\) percentile = \(\mathrm{111.2\,cm}\), \(\mathrm{97^{th}}\) percentile = \(\mathrm{115.0\,cm}\) (\(\mathrm{114\,cm}\) is between these)
- Age \(\mathrm{4:9}\): \(\mathrm{85^{th}}\) percentile = \(\mathrm{113.0\,cm}\), \(\mathrm{97^{th}}\) percentile = \(\mathrm{116.8\,cm}\) (\(\mathrm{114\,cm}\) is just above \(\mathrm{85^{th}}\))
- Age \(\mathrm{5:0}\): \(\mathrm{85^{th}}\) percentile = \(\mathrm{114.8\,cm}\) (\(\mathrm{114\,cm}\) is BELOW the \(\mathrm{85^{th}}\) percentile)
- Critical Finding: For a boy aged \(\mathrm{5:0}\) who is \(\mathrm{114\,cm}\) tall, he would be shorter than the \(\mathrm{85^{th}}\) percentile
- Counterexample: This boy is NOT taller than 85% of boys his age
- Reasoning: Since the statement must be true for ANY boy who is \(\mathrm{114\,cm}\) tall, and we found a counterexample, the statement is false
- Conclusion: NO
Systematic Checking
Each evaluation was verified against the appropriate data source with careful attention to percentile interpretations and age-specific growth patterns. The analysis confirms that statements 1 and 2 are supported by the percentile data, while statement 3 fails due to age-dependent height variations that create scenarios where the claim does not hold universally.
Final Answer
- Statement 1: Yes
- Statement 2: Yes
- Statement 3: No
If his age is greater than 3 years 3 months, the probability that his height is at least 98.0 cm is greater than 50%.
If he is at least 105 cm tall, the probability that his weight is 14.0 kg is no greater than 3%
If he is 114 cm tall, he is taller than at least 85% of boys his age.