The two graphs show the probability of having moved (changed residence) within the past 10 years by percentiles of per...
GMAT Graphics Interpretation : (GI) Questions
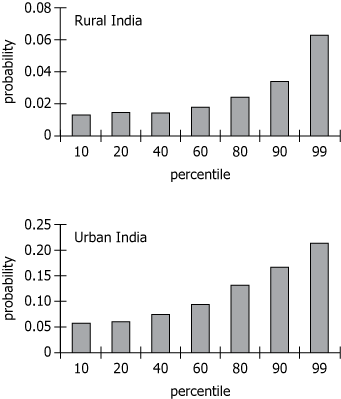
The two graphs show the probability of having moved (changed residence) within the past 10 years by percentiles of per capita consumption for individuals in rural and urban India. Note that the probability scales on the two graphs are different.
Use the drop-down menus to create statements that are consistent with the information presented.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Data subject | Probability of having moved (changed residence) within the past 10 years | The data is about how many people moved homes in the last decade |
| Grouping variable | Percentiles of per capita consumption | Population is divided by spending levels (poorer to richer groups) |
| Place of residence | Individuals in rural and urban India | The comparison is between rural and urban areas in India |
| Scale note | Note that the probability scales on the two graphs are different | The charts use different y-axis ranges (rural vs. urban) for better clarity |
Table 2: Chart Analysis
| Chart Component | What's Shown | Interpretation |
|---|---|---|
| Number of charts | Two bar charts: one for rural India, one for urban India | Enables direct rural-urban comparison of migration rates |
| X-axis | Percentiles: 10, 20, 40, 60, 80, 90, 99 (per capita consumption brackets) | Progresses from poorest to richest groups |
| Y-axis | Probability of having moved (Rural: \(0-0.08\); Urban: \(0-0.25\)) | Urban chart covers higher probability range, indicating more urban mobility |
| Bar heights | Rural: \(\sim 0.012\) (\(10^{\mathrm{th}}\)) to \(\sim 0.065\) (\(99^{\mathrm{th}}\)); Urban: \(0.06\) (\(10^{\mathrm{th}}\)) to \(0.22\) (\(99^{\mathrm{th}}\)) | At each percentile, migration is higher in urban India |
| Trend | Upward in both charts; steeper in urban, especially after \(80^{\mathrm{th}}\) percentile | Richer people move more; especially true in cities |
Key Insights
- Urban Indians at all income levels are much more likely to have moved than their rural counterparts; even the lowest urban migration probability (\(0.06\)) is nearly the highest in rural (\(0.065\)).
- Migration probabilities rise with higher consumption percentiles in both areas, but the increase is much sharper in urban India, especially among the top \(20\%\).
- The difference between rich and poor in terms of migration is much more dramatic in urban India (range \(\sim 0.16\)) than in rural India (range \(\sim 0.053\)), indicating greater mobility inequality in cities.
Step-by-Step Solution
Question 1: Comparison of \(99^{\mathrm{th}}\) Percentile Migration Probabilities
Complete Statement:
For individuals at the \(99^{\mathrm{th}}\) percentile of the per capita consumption distribution, the probability of having moved within the past 10 years for rural India is [blank] that for urban India.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: \(99^{\mathrm{th}}\) percentile of the per capita consumption distribution
- Meaning: Refers to people who are at the top \(1\%\) of per capita consumption (richest group).
- Relation to Chart: Focus on the \(99^{\mathrm{th}}\) percentile bar for both rural and urban India charts.
- Important Implications: We're comparing the richest groups in both settings.
- Statement Breakdown 2:
- Key Phrase: probability of having moved within the past 10 years
- Meaning: The fraction of people who changed their residence in the past decade.
- Relation to Chart: This is represented by the height of the bar for each percentile.
- Important Implications: Higher probability means more mobility.
What is needed: Whether rural India's probability at the \(99^{\mathrm{th}}\) percentile is less than, equal to, or greater than urban India's probability at the same percentile.
Solution:
- Condensed Solution Implementation:
Read off the values for the \(99^{\mathrm{th}}\) percentile from both charts and compare them. - Necessary Data points:
Rural India (\(99^{\mathrm{th}}\) percentile): \(\sim 0.065\). Urban India (\(99^{\mathrm{th}}\) percentile): \(\sim 0.22\). - Calculations Estimations:
\(0.065\) (rural) is less than \(0.22\) (urban). - Comparison to Answer Choices:
Since \(0.065 < 0.22\), the answer is 'less than'.
FINAL ANSWER Blank 1: less than
Question 2: Comparison of Ranges of Migration Probabilities
Complete Statement:
The range of the probability of having moved within the past 10 years for urban India is [blank] that for rural India.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: range of the probability
- Meaning: The difference between the highest and lowest probabilities.
- Relation to Chart: Subtract the minimum value from the maximum value for each group.
- Statement Breakdown 2:
- Key Phrase: urban India is [blank] that for rural India
- Meaning: We are comparing the range of urban India with the range of rural India.
- Relation to Chart: Compare the calculated range values between urban and rural India.
What is needed: Whether the range in urban India is less than, equal to, or greater than the range in rural India.
Solution:
- Condensed Solution Implementation:
Calculate the minimum and maximum values for each and find the difference, then compare. - Necessary Data points:
Rural India: min \(\sim 0.012\), max \(\sim 0.065\) (range = \(0.065 - 0.012 = 0.053\)). Urban India: min \(\sim 0.06\), max \(\sim 0.22\) (range = \(0.22 - 0.06 = 0.16\)). - Calculations Estimations:
\(0.16\) (urban range) is greater than \(0.053\) (rural range). - Comparison to Answer Choices:
Since \(0.16 > 0.053\), the answer is 'greater than'.
FINAL ANSWER Blank 2: greater than
Summary
For the \(99^{\mathrm{th}}\) percentile, rural India's migration probability is less than that of urban India (\(0.065\) vs \(0.22\)). The range of migration probabilities is greater for urban India (\(0.16\)) than for rural India (\(0.053\)), indicating more variation among urban residents.
Question Independence Analysis
The two questions are independent. Question 1 asks about the \(99^{\mathrm{th}}\) percentile specifically, while Question 2 asks about the difference between the maximum and minimum values overall. The answer to one does not affect the other.