The hail events in a certain region are classified by the diameter of the largest hail stone measured in the...
GMAT Graphics Interpretation : (GI) Questions
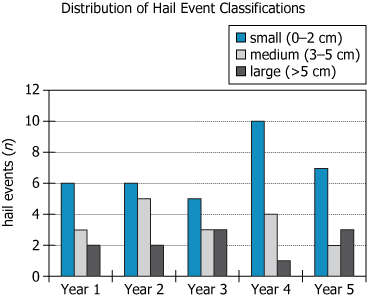
The hail events in a certain region are classified by the diameter of the largest hail stone measured in the event: small (\(0\text{–}2\text{ cm}\)), medium (\(3\text{–}5\text{ cm}\)), and large (\(> 5\text{ cm}\)). The graph shows the distribution of classifications of all of the hail events in this region over the span of 5 years.
Select from each drop-down menu the option that creates the most accurate statement based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Subject | The hail events in a certain region | Data concerns hail events (storms with hail) in a single region |
| Measurement | classified by the diameter of the largest hail stone measured in the event | Each event is categorized by the diameter of the largest hailstone |
| Size Classes | small (\(0-2\) cm), medium (\(3-5\) cm), and large (\(\gt 5\) cm) | Three categories: small (up to 2 cm), medium (3-5 cm), large (greater than 5 cm) |
| Data Scope | distribution of classifications of all of the hail events | The data shows how many events fall into each size classification |
| Time Frame | over the span of 5 years | The dataset covers 5 consecutive years |
Table 2: Chart Analysis
| Chart Component | What is Presented | What it Shows |
|---|---|---|
| Chart Type | Grouped bar chart for 5 years | Allows comparison of different hail sizes each year |
| X-axis | Year 1 to Year 5 | 5 distinct years analyzed |
| Y-axis | Scale 0-12, labeled 'Hail events' | Number of hail events per size category, per year |
| Bar Groups | Three colors/bars per year: blue (small), white/light (medium), gray (large) | Each year, distribution among small/medium/large sizes visualized |
| Data Values | Year 1: \(6/3/2\), Year 2: \(6/5/2\), Year 3: \(5/3/3\), Year 4: \(10/4/1\), Year 5: \(7/2/3\) (small/medium/large respectively) | Number of events by type for each year, used for trend analysis |
| Totals | Year 1: \(11\), Year 2: \(13\), Year 3: \(11\), Year 4: \(15\), Year 5: \(12\) | Year 4 has the highest total event count |
Key Insights
Year 4 stands out with the highest total number of hail events (\(15\)) driven primarily by a sharp rise in small hail events (\(10\)). It also saw the fewest large hail events (\(1\)) among all years, creating an inverse relationship between small and large hail frequencies in that year. In general, annual totals are driven most by small hail events, while medium and large categories vary less dramatically. Year 2 displayed the most balanced distribution among the three size types.
Step-by-Step Solution
Question 1: Determining the Hail Size Category With the Most Events in the Maximum Year
Complete Statement:
Of the years reflected in the graph, the year when this region had the greatest total number of hail events was the year when this region had the greatest number of [BLANK 1] hail events and the least number of [BLANK 2] hail events.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: the year when this region had the greatest total number of hail events
- Meaning: Find the year where the combined number of all sizes of hail events is largest.
- Relation to Chart: Year 4 has the highest total hail events (\(15\)).
- Important Implications: Year 4 is the focus year for the rest of the question.
- Statement Breakdown 2:
- Key Phrase: the greatest number of [BLANK 1] hail events
- Meaning: Of the three size categories (small, medium, large), determine which had the highest count in Year 4.
- Relation to Chart: In Year 4: small=\(10\), medium=\(4\), large=\(1\).
- Important Implications: The category with the largest value in Year 4 fills BLANK 1.
What is needed: Which size category of hail events had the largest number during the year with the most total hail events.
Solution:
- Condensed Solution Implementation:
From the chart analysis, compare counts of small, medium, and large hail in Year 4 and select the largest. - Necessary Data points:
Year 4: small=\(10\), medium=\(4\), large=\(1\). - Calculations Estimations:
\(10\) (small) \(\gt 4\) (medium) \(\gt 1\) (large) — so small hail events had the highest count. - Comparision to Answer Choices:
"small" matches the highest value.
FINAL ANSWER Blank 1: small
Question 2: Determining the Hail Size Category With the Fewest Events in the Maximum Year
Complete Statement:
Of the years reflected in the graph, the year when this region had the greatest total number of hail events was the year when this region had the greatest number of small hail events and the least number of [BLANK 2] hail events.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: the least number of [BLANK 2] hail events
- Meaning: Of the three size categories, find which had the lowest count in Year 4.
- Relation to Chart: In Year 4: small=\(10\), medium=\(4\), large=\(1\).
- Statement Breakdown 2:
- Key Phrase: ****
- Meaning:
- Relation to Chart:
What is needed: Which size category of hail events had the smallest number during the year with the most total hail events.
Solution:
- Condensed Solution Implementation:
Look at the counts for small, medium, large in Year 4 and find the smallest. - Necessary Data points:
Year 4: small=\(10\), medium=\(4\), large=\(1\). - Calculations Estimations:
\(1\) (large) \(\lt 4\) (medium) \(\lt 10\) (small) — so large hail events had the lowest count. - Comparision to Answer Choices:
"large" matches the lowest value.
FINAL ANSWER Blank 2: large
Summary
Year 4 had the greatest total number of hail events (\(15\)). In that year, small hail events were the most common (\(10\) occurrences), while large hail events were the least common (only \(1\) occurrence). Thus, 'small' fills the first blank and 'large' the second.
Question Independence Analysis
The blanks are closely dependent since each refers to a specific statistic (most and least) within the same year (the year with the greatest total number of hail events, Year 4). Knowledge of Year 4's data is necessary for both answers.