The graph shows the total energy usage in kilowatt hours (kWh) for a small retail business for each month of...
GMAT Graphics Interpretation : (GI) Questions
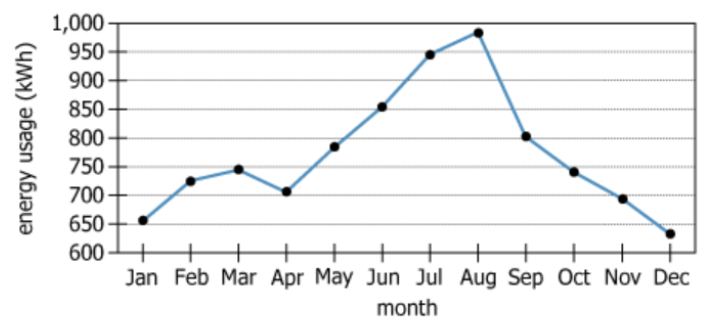
The graph shows the total energy usage in kilowatt hours (kWh) for a small retail business for each month of last year. The business owner is interested in comparing the business's median monthly energy usage per quarter among Quarter 1 (January through March), Quarter 2 (April through June), Quarter 3 (July through September), and Quarter 4 (October through December).
Select from the drop-down menus the options that create the sentence that most accurately reflects the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Subject | The graph shows the total energy usage in kilowatt hours \(\mathrm{(kWh)}\) for a small retail business | We're analyzing energy consumption for a small store |
| Time Period | Each month of last year | Data includes all 12 months (Jan–Dec) from previous year |
| Measurement Unit | Kilowatt hours \(\mathrm{(kWh)}\) | Standard electricity usage unit |
| Analysis Focus | Comparing the business's median monthly energy usage per quarter | The central value (median) is determined for each quarter |
| Quarter Definitions | Q1: Jan–Mar, Q2: Apr–Jun, Q3: Jul–Sep, Q4: Oct–Dec | Quarters split the year into four three-month blocks |
Table 2: Chart Analysis
| Chart Component | What's Shown | Interpretation |
|---|---|---|
| Chart Type | Single line chart with 12 points | Depicts monthly energy use progression |
| X-Axis | Months (January–December) | Represents time throughout the year |
| Y-Axis | Energy usage in \(\mathrm{kWh}\) (approx. 600–1000 \(\mathrm{kWh}\)) | Shows monthly consumption scale |
| Data Pattern | Peaks in July–August (Q3), lowest at December (Q4) | Indicates strong summer energy demand and winter low |
| Quarterly Summary | Q3 highest median (\(\mathrm{940\;kWh}\)), Q4 lowest (\(\mathrm{690\;kWh}\)) | Matches observed seasonal energy trends |
Key Insights
There is strong seasonality in energy usage for the small retail business: Quarter 3 (summer) has the highest median monthly energy use at \(\mathrm{940\;kWh}\), while Quarter 4 (winter) is lowest at \(\mathrm{690\;kWh}\). This \(\mathrm{250\;kWh}\) gap underscores significant seasonal shifts in energy demand, with consumption peaking in the summer and dipping in the winter months.
Step-by-Step Solution
Question 1: Identifying the Quarter with the Greatest Median Energy Usage
Complete Statement:
Among the quarterly medians (the medians of the business's monthly energy usages for each quarter), the greatest quarterly median was for Quarter [BLANK 1]
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: quarterly medians
- Meaning: Find the median (middle value) of energy usage for each quarter.
- Relation to Chart: Each quarter has three months' data; arrange each set of three monthly usages in order to get the median for that quarter.
- Important Implications: We will have four numbers (one for each quarter) to compare and identify the largest.
- Statement Breakdown 2:
- Key Phrase: the greatest quarterly median
- Meaning: Select the largest among the four computed medians.
- Relation to Chart: Use the previously computed medians from each quarter.
- Important Implications: Determines which quarter to report in BLANK 1.
- What is needed: Which quarter (1, 2, 3, or 4) had the highest median of its three monthly usages.
Solution:
- Condensed Solution Implementation:
Calculate the median monthly usage in each quarter, then compare to find the greatest. - Necessary Data points:
Q1: Jan 660, Feb 725, Mar 745; Q2: Apr 710, May 780, Jun 860; Q3: Jul 940, Aug 980, Sep 810; Q4: Oct 740, Nov 690, Dec 630.- Calculations Estimations:
\(\mathrm{Q1\;(660, 725, 745): Median = 725}\). \(\mathrm{Q2\;(710, 780, 860): Median = 780}\). \(\mathrm{Q3\;(810, 940, 980): Median = 940}\). \(\mathrm{Q4\;(630, 690, 740): Median = 690}\). - Comparison to Answer Choices:
Medians are Q1: 725, Q2: 780, Q3: 940, Q4: 690. The greatest is Q3.
- Calculations Estimations:
FINAL ANSWER Blank 1: 3
Question 2: Determining How Much the Greatest Median Exceeds the Least Median
Complete Statement:
...and that quarterly median exceeded the least quarterly median by [BLANK 2] \(\mathrm{kWh}\), to the nearest 50 \(\mathrm{kWh}\)
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: exceeded the least quarterly median
- Meaning: Subtract the smallest quarterly median from the greatest.
- Relation to Chart: Compare the largest and smallest values among the four medians.
- Statement Breakdown 2:
- Key Phrase: to the nearest 50 \(\mathrm{kWh}\)
- Meaning: Round the answer to the closest multiple of 50.
- Relation to Chart: Round the computed difference if necessary.
- What is needed: By how much (rounded to the nearest 50 \(\mathrm{kWh}\)) the greatest median is higher than the least median.
Solution:
- Condensed Solution Implementation:
Subtract the least median from the greatest and round appropriately. - Necessary Data points:
Greatest median: 940 (Q3), least median: 690 (Q4).- Calculations Estimations:
\(\mathrm{940 - 690 = 250\;kWh}\). - Comparison to Answer Choices:
250 is already a multiple of 50 and matches a possible answer.
- Calculations Estimations:
FINAL ANSWER Blank 2: 250
Summary
First, calculate each quarter's median monthly usage and compare to identify Quarter 3 (Q3) as the greatest. Then, find the difference between the greatest (940) and least (690) quarterly medians to get \(\mathrm{250\;kWh}\) (already rounded).
Question Independence Analysis
The questions are dependent: the second asks about the difference between 'that quarterly median' found in the first, requiring the first answer to solve the second.