The graph shows the maximum absolute humidity—the maximum amount of water vapor that atmospheric air at sea level can hold—in...
GMAT Graphics Interpretation : (GI) Questions
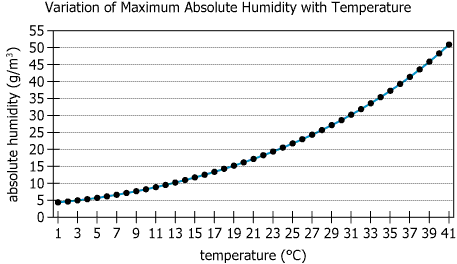
The graph shows the maximum absolute humidity—the maximum amount of water vapor that atmospheric air at sea level can hold—in grams of water vapor per cubic meter (\(\mathrm{g/m^3}\)), for integer-valued temperatures on the Celsius scale from \(1°\mathrm{C}\) through \(41°\mathrm{C}\). When the air contains this maximum amount of water vapor, the air is said to be at its saturation point. In addition, at sea level and at a temperature of \(T°\mathrm{C}\), the density of air containing no water vapor is \(\frac{10^5}{287(T + 273)}\) \(\mathrm{kg/m^3}\) where \(1\) kg \(= 1\) kilogram \(= 1,000\) g.
From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Graph subject matter | "The graph shows the maximum absolute humidity" | The chart displays how much water vapor air can hold at different temperatures |
| Definition of maximum absolute humidity | "the maximum amount of water vapor that atmospheric air at sea level can hold—in grams of water vapor per cubic meter (g/m^3)" | Maximum water vapor is measured in grams per cubic meter of air |
| Temperature range | "for integer-valued temperatures on the Celsius scale from \(1°\text{C}\) through \(41°\text{C}\)" | Data covers every whole number temperature from 1 to 41 degrees Celsius |
| Saturation point definition | "When the air contains this maximum amount of water vapor, the air is said to be at its saturation point." | Saturation point means air holds all the water vapor it possibly can |
| Dry air density formula | "at sea level and at a temperature of T °C, the density of air containing no water vapor is \(\frac{10^5}{287(T + 273)} \text{ kg/m}^3\)" | There's a formula to calculate how much dry air weighs at any temperature |
| Unit conversion | "1 kg = 1 kilogram = 1,000 g" | 1 kilogram equals 1,000 grams |
Table 2: Chart Analysis
| Chart Component | What's Shown | What This Tells Us |
|---|---|---|
| Chart type | Line graph with circular markers (continuous curve) | The data varies smoothly and continuously across the temperature range |
| X-axis | Temperature in °C from 1 to 41, odd numbers labeled | Covers all integer degrees within the stated range |
| Y-axis | Maximum absolute humidity in g/m^3 from 0 to 55 | Shows water vapor amounts up to 55 grams per cubic meter |
| Curve shape | Steep upward curve, especially rapid above \(30°\text{C}\) | Air's water vapor capacity increases more rapidly at higher temperatures |
| Sample data points | At \(1°\text{C}\): ~4 g/m^3, \(21°\text{C}\): ~16 g/m^3, \(31°\text{C}\): ~30 g/m^3, \(41°\text{C}\): ~51 g/m^3 | Shows more than 12-fold increase in maximum humidity from \(1°\text{C}\) to \(41°\text{C}\) |
Key Insights
- The dataset illustrates the exponential relationship between temperature and air's water vapor capacity: as temperature rises, especially above \(30°\text{C}\), maximum humidity increases rapidly.
- The formula for dry air density enables comparison of dry air mass to maximum possible water vapor at each temperature, supporting percentage-based calculations.
- All data is specific to atmospheric air at sea level, both for humidity values and air density.
- The full integer temperature spectrum from \(1°\text{C}\) to \(41°\text{C}\) supports granular analysis of humidity changes across small temperature intervals.
Step-by-Step Solution
Question 1: Calculating the Percentage of Water Vapor at \(37°\text{C}\)
Complete Statement:
At \(37°\text{C}\), and at sea level, the weight of water vapor in \(1 \text{ m}^3\) of air at its saturation point is [BLANK] % of the weight of \(1 \text{ m}^3\) of air containing no water vapor.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: At \(37°\text{C}\), and at sea level
Meaning: The calculation focuses on conditions at exactly \(37°\text{C}\) and sea-level atmospheric pressure.
Relation to Chart: We need to use the data point from the chart at \(37°\text{C}\), which is based on sea-level pressure.
Important Implications: All values and calculations must apply to the row or data for \(37°\text{C}\) on the chart.
- Key Phrase: At \(37°\text{C}\), and at sea level
- Statement Breakdown 2:
- Key Phrase: weight of water vapor in \(1 \text{ m}^3\) of air at its saturation point
Meaning: The amount (mass) of water vapor air can hold at maximum (fully saturated) at \(37°\text{C}\).
Relation to Chart: Read directly as the 'maximum absolute humidity' at \(37°\text{C}\) from the chart.
Important Implications: This is the numerator in the percentage calculation.
- Key Phrase: weight of water vapor in \(1 \text{ m}^3\) of air at its saturation point
What is needed: The percentage ratio (by mass) of saturated water vapor to dry air in \(1 \text{ m}^3\) at \(37°\text{C}\).
Solution:
- Condensed Solution Implementation:
Use the value from the chart for water vapor at \(37°\text{C}\), then compute dry air density for \(1 \text{ m}^3\) using the provided formula; compute the ratio and convert to percent. - Necessary Data points:
Maximum absolute humidity at \(37°\text{C}\) from the chart: 40 g/m³; dry air density from the formula: \(\frac{10^5}{287 \times (37 + 273)}\).- Calculations Estimations:
Dry air density: \(\frac{10^5}{287 \times 310} = \frac{10^5}{88970} \approx 1.124 \text{ kg/m}^3 = 1124 \text{ g/m}^3\). Percentage = \(\frac{40 \text{ g/m}^3}{1124 \text{ g/m}^3} \times 100\% \approx 3.6\%\). - Comparison to Answer Choices:
3.6% matches one of the answer choices (3.0%, 3.6%, 4.0%, 4.2%).
- Calculations Estimations:
FINAL ANSWER Blank 1: 3.6
Question 2: Comparing Rates of Change in Maximum Absolute Humidity
Complete Statement:
The average rate of change of maximum absolute humidity from \(31°\text{C}\) to \(41°\text{C}\) is [BLANK] the average rate of change of maximum absolute humidity from \(11°\text{C}\) to \(21°\text{C}\).
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: average rate of change of maximum absolute humidity from \(31°\text{C}\) to \(41°\text{C}\)
Meaning: How much the maximum absolute humidity increases per degree Celsius between \(31°\text{C}\) and \(41°\text{C}\).
Relation to Chart: Obtain absolute humidity values at \(31°\text{C}\) and \(41°\text{C}\) from the chart to calculate the rate.
- Key Phrase: average rate of change of maximum absolute humidity from \(31°\text{C}\) to \(41°\text{C}\)
- Statement Breakdown 2:
- Key Phrase: average rate of change ... from \(11°\text{C}\) to \(21°\text{C}\)
Meaning: How much maximum absolute humidity increases per degree Celsius between \(11°\text{C}\) and \(21°\text{C}\).
Relation to Chart: Obtain absolute humidity values at \(11°\text{C}\) and \(21°\text{C}\) from the chart to calculate this rate.
- Key Phrase: average rate of change ... from \(11°\text{C}\) to \(21°\text{C}\)
What is needed: Whether the first rate of change (\(31°\text{C}\)–\(41°\text{C}\)) is greater than, less than, or about the same as the second rate (\(11°\text{C}\)–\(21°\text{C}\)).
Solution:
- Condensed Solution Implementation:
Calculate the average rates for both intervals using the differences in maximum absolute humidity values from the chart, then compare. - Necessary Data points:
From the chart: at \(31°\text{C}\): 30 g/m³; at \(41°\text{C}\): 51 g/m³; at \(11°\text{C}\): 9 g/m³; at \(21°\text{C}\): 16 g/m³.- Calculations Estimations:
\(31°\text{C}\)-\(41°\text{C}\): \(\frac{51 - 30}{41 - 31} = \frac{21}{10} = 2.1 \text{ g/m}^3/°\text{C}\). \(11°\text{C}\)-\(21°\text{C}\): \(\frac{16 - 9}{21 - 11} = \frac{7}{10} = 0.7 \text{ g/m}^3/°\text{C}\). - Comparison to Answer Choices:
2.1 is much greater than 0.7, so the answer is 'greater than'.
- Calculations Estimations:
FINAL ANSWER Blank 2: greater than
Summary
Blank 1 required a direct calculation of percentage using the graph value and air density formula, resulting in 3.6%. Blank 2 involved comparing the steepness (rate of increase) of the humidity curve at high and low temperature intervals, with the increase being much greater at higher temperatures; thus, the answer is 'greater than'.
Question Independence Analysis
Blank 1 and blank 2 are independent: blank 1 asks for a calculation at a single temperature, while blank 2 asks for a comparison of rates over two different temperature intervals. The answer to one does not depend on the answer to the other.