The graph shows the maximum absolute humidity—the maximum amount of water vapor that atmospheric air at sea level can hold—in...
GMAT Graphics Interpretation : (GI) Questions
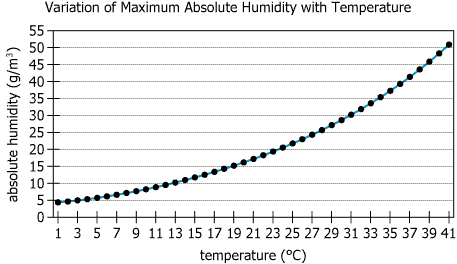
The graph shows the maximum absolute humidity—the maximum amount of water vapor that atmospheric air at sea level can hold—in grams of water vapor per cubic meter (\(\mathrm{g/m^3}\)), for integer-valued temperatures on the Celsius scale from 1°C through 41°C. When the air contains this maximum amount of water vapor, the air is said to be at its saturation point. In addition, at sea level and at a temperature of \(\mathrm{T °C}\), the density of air containing no water vapor is \(\frac{10^5}{287(T + 273)} \mathrm{kg/m^3}\) where 1 kg = 1 kilogram = 1,000 g.
From each drop-down menu, select the option that creates the most accurate statement according to the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Description | Simplified Meaning |
|---|---|---|
| Overview | The graph shows maximum absolute humidity (grams of water vapor per cubic meter) for sea-level air at temperatures \(1°\mathrm{C}\) to \(41°\mathrm{C}\). | The dataset details how much water air can maximally hold at different temperatures, at sea level. |
| Definition | 'Saturation point' when air holds this maximum water. | Air can't hold more vapor at this state. |
| Formula | Dry air density at sea level: \(\frac{10^5}{287(\mathrm{T}+273)} \text{ kg/m}^3\) | There's a method to calculate the mass of \(1 \text{ m}^3\) dry air at any temperature. |
| Units | Water measured in grams (g); air density in kilograms (kg), with \(1 \text{ kg} = 1000 \text{ g}\). | All values can be compared directly via these units. |
Table 2: Chart Analysis
| Chart Element | What It Shows | Interpretation |
|---|---|---|
| Type | Scatter plot connected by a line, 41 data points (temperatures \(1°\mathrm{C}\) to \(41°\mathrm{C}\)) | Temperature increments are every \(1°\mathrm{C}\) (likely every integer value). |
| X-axis | Temperature (°C), 1–41 | Temperature is the independent variable. |
| Y-axis | Maximum absolute humidity (g/m³), 0–55 | Humidity rises as temperature increases. |
| Curve Shape | Exponential rise, nearly flat at low T, rapid increase above \(30°\mathrm{C}\) | Small increases at low T, sharp increases at high T. |
| Key Data | Values: \(1°\mathrm{C}\)–4g, \(11°\mathrm{C}\)–9g, \(21°\mathrm{C}\)–16g, \(31°\mathrm{C}\)–30g, \(37°\mathrm{C}\)–40g, \(41°\mathrm{C}\)–51g | Humidity capacity at \(41°\mathrm{C}\) is over 12× that at \(1°\mathrm{C}\). |
| Growth Comparison | \(11→21°\mathrm{C}: +7\text{g/m}³\); \(31→41°\mathrm{C}: +21\text{g/m}³\) | Rate of increase grows rapidly with temperature. |
Key Insights
The maximum absolute humidity of air increases exponentially with temperature at sea level. Between \(1°\mathrm{C}\) and \(21°\mathrm{C}\), water vapor capacity rises modestly, but above \(30°\mathrm{C}\), the air's capacity for water vapor increases dramatically. From \(31°\mathrm{C}\) to \(41°\mathrm{C}\), the additional water vapor air can hold grows three times faster than from \(11°\mathrm{C}\) to \(21°\mathrm{C}\) (\(21\text{g/m}³\) vs \(7\text{g/m}³\) increase). At \(37°\mathrm{C}\)—the body's typical temperature—water vapor at saturation is about \(3.6\%\) of the weight of \(1 \text{ m}^3\) of dry air. The chart highlights that hot air can carry much more moisture than cold air, and the underlying dataset provides values at each integer temperature from \(1°\mathrm{C}\) to \(41°\mathrm{C}\) for full quantitative analysis.
Step-by-Step Solution
Question 1: Water Vapor Percentage by Weight at 37°C
Complete Statement:
At \(37°\mathrm{C}\), and at sea level, the weight of water vapor in \(1 \text{ m}^3\) of air at its saturation point is ___%of the weight of \(1 \text{ m}^3\) of air containing no water vapor.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: At \(37°\mathrm{C}\), and at sea level
- Meaning: This sets the specific temperature and conditions for the calculation.
- Relation to Chart: We need to find the value at \(37°\mathrm{C}\) from the chart (maximum absolute humidity).
- Important Implications: All calculations will use values at \(37°\mathrm{C}\) from the provided data/chart.
- Statement Breakdown 2:
- Key Phrase: weight of water vapor in \(1 \text{ m}^3\) of air at its saturation point
- Meaning: The amount (in grams) of water vapor at maximum (saturated) humidity at this temperature in one cubic meter of air.
- Relation to Chart: Read the maximum absolute humidity at \(37°\mathrm{C}\) from the chart/table.
- Important Implications: This gives us the numerator in the percentage calculation.
- What is needed: At \(37°\mathrm{C}\), the percentage of the mass of saturated water vapor per m³ compared to the mass of dry air per m³.
Solution:
- Condensed Solution Implementation:
Use the given dry air density equation and saturated vapor data from the chart to compute the percentage. - Necessary Data points:
Max absolute humidity at \(37°\mathrm{C}\): \(40 \text{ g/m}^3\). Dry air density at \(37°\mathrm{C}\) from formula: \(\frac{10^5}{287 × (37 + 273)}\).- Calculations Estimations:
Calculate dry air density: \(\frac{10^5}{287 × 310} = \frac{100000}{88970} ≈ 1.12 \text{ kg/m}^3 = 1120 \text{ g/m}^3\). Calculate percentage: \(\frac{40}{1120} × 100\% ≈ 3.57\%\). - Comparison to Answer Choices:
Choices are typically to one decimal. \(3.57\%\) rounds to \(3.6\%\), so the answer is 3.6.
- Calculations Estimations:
FINAL ANSWER Blank 1: 3.6
Question 2: Comparing Rates of Change of Maximum Absolute Humidity
Complete Statement:
The average rate of change of maximum absolute humidity from \(31°\mathrm{C}\) to \(41°\mathrm{C}\) is ___ the average rate of change of maximum absolute humidity from \(11°\mathrm{C}\) to \(21°\mathrm{C}\).
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: average rate of change of maximum absolute humidity from \(31°\mathrm{C}\) to \(41°\mathrm{C}\)
- Meaning: How much, on average, the humidity increases for each \(1°\mathrm{C}\) in this temperature range.
- Relation to Chart: Find the values at \(31°\mathrm{C}\) and \(41°\mathrm{C}\) in the chart, subtract, and divide by the temperature difference.
- Statement Breakdown 2:
- Key Phrase: average rate of change of maximum absolute humidity from \(11°\mathrm{C}\) to \(21°\mathrm{C}\)
- Meaning: How much, on average, the humidity increases for each \(1°\mathrm{C}\) in the lower temperature range.
- Relation to Chart: Find the values at \(11°\mathrm{C}\) and \(21°\mathrm{C}\) in the chart, subtract, and divide by the temperature difference.
- What is needed: Whether the average rate of increase in humidity per degree is greater at higher or lower temperatures.
Solution:
- Condensed Solution Implementation:
Calculate the difference in humidity over each interval and divide by the number of degrees (10), then compare the two results. - Necessary Data points:
From the chart: \(11°\mathrm{C} = 9 \text{ g/m}^3\), \(21°\mathrm{C} = 16 \text{ g/m}^3\), \(31°\mathrm{C} = 30 \text{ g/m}^3\), \(41°\mathrm{C} = 51 \text{ g/m}^3\).- Calculations Estimations:
From \(11°\mathrm{C}\) to \(21°\mathrm{C}\): \(\frac{16 - 9}{10} = 0.7 \text{ g/m}^3\) per \(°\mathrm{C}\). From \(31°\mathrm{C}\) to \(41°\mathrm{C}\): \(\frac{51 - 30}{10} = 2.1 \text{ g/m}^3\) per \(°\mathrm{C}\). - Comparison to Answer Choices:
2.1 is much greater than 0.7, so the correct comparison is 'greater than.'
- Calculations Estimations:
FINAL ANSWER Blank 2: greater than
Summary
Blank 1 is solved by comparing the mass of saturated water vapor at \(37°\mathrm{C}\) to the mass of dry air at the same temperature, giving \(3.6\%\). Blank 2 is solved by comparing the average rate of change of maximum absolute humidity in different temperature ranges; the rate between \(31°\mathrm{C}\) and \(41°\mathrm{C}\) is much greater than that between \(11°\mathrm{C}\) and \(21°\mathrm{C}\).
Question Independence Analysis
The two blanks are independent: Blank 1 asks for a ratio at a single temperature (\(37°\mathrm{C}\)), while Blank 2 compares average rates of humidity change in two separate temperature intervals. Solving one does not require information from the other.