The graph shows the distributions of scores on official driving tests administered within a certain municipality for eight consecutive business...
GMAT Graphics Interpretation : (GI) Questions
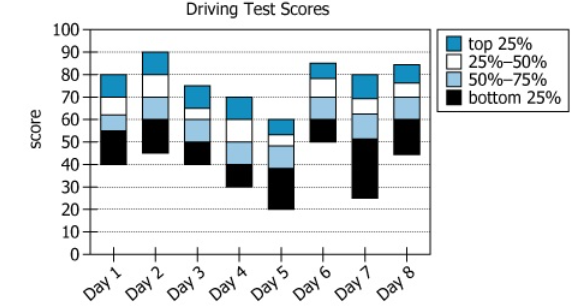
The graph shows the distributions of scores on official driving tests administered within a certain municipality for eight consecutive business days.
Select from each drop-down menu the option that creates the most accurate statement, given the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Content |
|---|---|
| Subject | Distributions of scores on official driving tests |
| Location | Administered within a certain municipality |
| Time Frame | Eight consecutive business days |
| Focus | Score distributions, not just averages |
Table 2: Chart Analysis
| Chart Component | Description |
|---|---|
| Chart Type | Stacked bar chart showing 8 days (Day 1-8); each bar divided into 4 quartiles |
| Y-Axis | Test scores from 0 to 100 |
| X-Axis | Days 1 through 8 |
| Quartile Segments | Each segment shows the score range for a quartile (bottom 25%, \\(\mathrm{25-50\%}\\), \\(\mathrm{50-75\%}\\), top 25%) per day |
| Range and Minimum/Maximum | Lowest minimum: Day 5 (score 20); highest maximum: Day 2 (score 90); overall range is 70 points |
Key Insights
The chart displays how test scores are distributed across eight sequential days, dividing each day's results into quartiles. The median score for each day sits at the boundary between the \\(\mathrm{25-50\%}\\) and \\(\mathrm{50-75\%}\\) segments. The overall range across all days is 70 points (from \\(\mathrm{20 \text{ to } 90}\\)), with this range fully captured by combining Day 2 and Day 5. While median and range are visually discernible, mean values for each day or group of days cannot be precisely determined from the chart alone.
Step-by-Step Solution
Question 1: Identifying the Statistical Measure from the Chart
Complete Statement:
The graph provides enough information to determine that the [mean score/median score/range of scores] over all of the days indicated in the graph is the same as that for [Day 1 and Day 8/Day 2 and Day 5/Day 3 and Day 7/Day 4 and Day 5] combined.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: The graph provides enough information to determine
- Meaning: We are to choose a statistic that can be directly evaluated from the provided chart.
- Relation to Chart: The chart shows distributions as quartiles (stacked bars), with the minimum, first quartile, median, third quartile, and maximum shown.
- Important Implications: Only statistics visible from the quartile summaries are valid answers; the mean cannot be computed precisely from quartile data.
- Statement Breakdown 2:
- Key Phrase: [mean score/median score/range of scores]
- Meaning: These are possible statistics to choose from.
- Relation to Chart: Median and range can be determined from quartiles; mean cannot.
- Important Implications: Mean cannot be calculated from only quartiles, but median and range can.
What is needed: Which statistic—mean, median, or range—can be both determined from quartile data and matches for all days and for some specific pair of days' combined scores.
Solution:
- Condensed Solution Implementation:
Review what can be determined from a quartile-based bar chart. The range (difference between max and min) is visible for each day and across all days. The mean cannot be determined; the median can be determined for each day, but not directly for the combined set. Thus, range is the answer. - Necessary Data points:
Chart provides explicit maximums and minimums for each day. The lowest minimum is 20 (Day 5), the highest maximum is 90 (Day 2), so the overall range is \\(\mathrm{90 - 20 = 70}\\) points. - Calculations Estimations:
Range across all days: \\(\mathrm{90 - 20 = 70}\\) points. - Comparison to Answer Choices:
Only the range of scores can be confirmed and compared in this way from the chart.
FINAL ANSWER Blank 1: range of scores
Question 2: Identifying Which Pair of Days Matches the Overall Range
Complete Statement:
The graph provides enough information to determine that the range of scores over all of the days indicated in the graph is the same as that for [Day 1 and Day 8/Day 2 and Day 5/Day 3 and Day 7/Day 4 and Day 5] combined.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: is the same as that for [Day pairs] combined
- Meaning: Asks which two days, when combined, have the same minimum and maximum as all days.
- Relation to Chart: Identify the days with the absolute minimum and maximum values from the chart.
What is needed: Which day pair contains both the lowest minimum (20) and the highest maximum (90), to achieve a 70-point range.
Solution:
- Condensed Solution Implementation:
Check each candidate pair to see if their combined minimum and maximum cover the full 20 to 90 range. - Necessary Data points:
Day 2: min 45, max 90. Day 5: min 20, max 60. Day 2 and Day 5 together have min 20 and max 90. - Calculations Estimations:
Combined range for Days 2 and 5: \\(\mathrm{90 - 20 = 70}\\) points. - Comparison to Answer Choices:
Only Day 2 and Day 5 span the full range; other pairs don't have both 20 and 90.
FINAL ANSWER Blank 2: Day 2 and Day 5
Summary
By reviewing how quartile data is presented in the chart, it becomes clear that the range of scores (maximum minus minimum) is the only statistic that can be directly calculated for all days and for a specific pair of days. Only Day 2 (max = 90) and Day 5 (min = 20) together match the overall range across all eight days.
Question Independence Analysis
The questions are dependent. The correct completion of the second blank depends on what statistic is chosen in the first blank. Once 'range of scores' is selected for the first blank, only one pair of days—Day 2 and Day 5—has the required minimum and maximum values for the second blank.