The graph shows the average (arithmetic mean) mature tree heights of each of Species A-C at each of the Tree...
GMAT Graphics Interpretation : (GI) Questions
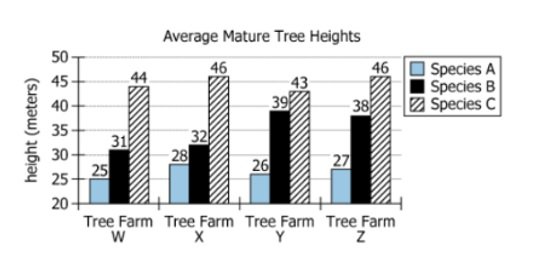
The graph shows the average (arithmetic mean) mature tree heights of each of Species A-C at each of the Tree Farms W-Z.
Based on the information provided, select from each drop-down menu the option that creates the most accurate statement.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Subject | The graph shows the average (arithmetic mean) mature tree heights | The focus is on tree heights after full growth, summarized by mean |
| Species | Each of Species A–C | Three tree types: A, B, C |
| Locations | At each of the Tree Farms W–Z | Data collected at four places: Farm W, X, Y, Z |
| Measurement | Average (arithmetic mean) mature height | For each species at each farm, average height was computed |
Table 2: Chart Analysis
| Chart Component | Description | Interpretation |
|---|---|---|
| Chart Type | Grouped bar chart for each farm | Three bars per farm make it easy to compare species at each location and across locations |
| Y-Axis | Label shows meters, from 0 to 50 | All measured heights (25–46 meters) are within the axis, easy to visually rank |
| X-Axis | Farms W, X, Y, Z (groups) | Organizes data by location, direct farm-to-farm comparison |
| Bar Series | Species A (solid), B (solid/black), C (striped) | Visual patterns distinguish the three species |
| Data Labels | Heights printed on top of each bar | Viewers can use precise figures instead of estimating |
| Notable Patterns | Species C always tallest, B changes notably at Farms Y/Z | C is consistently highest; B jumps from 31 to 38 meters at some farms |
Key Insights
Farm Z has the greatest sum of average mature tree heights for all three species (sum: \(27 + 38 + 46 = 111\) meters). Species B has the greatest standard deviation of the four average mature heights, since it is 31 at Farms W and X, then jumps to 38 at Farms Y and Z (more variability than A or C). Species C is always the tallest species at each farm and remains fairly consistent (43–46 meters), while Species A varies the least, ranging only from 25–28 meters.
Step-by-Step Solution
Question 1: Sum of Average Mature Heights Across Farms
Complete Statement:
For the 4 tree farms, the sum of the average mature heights of Species A, B, and C is greatest for Tree Farm ______.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: sum of the average mature heights
- Meaning: Add together the average heights of three species (A, B, and C).
- Relation to Chart: On the chart, these are the three bars for each farm. Their individual values must be summed for each farm.
- Important Implications: We'll need to sum the values for each farm and then compare them.
- Statement Breakdown 2:
- Key Phrase: greatest for Tree Farm _____
- Meaning: The question is asking at which farm the summed height is at its highest.
- Relation to Chart: Compare the totals across all four farms (W, X, Y, and Z).
- Important Implications: Identify the farm with the absolute highest combined height.
- What is needed: Which farm, among W, X, Y, and Z, has the largest sum when you add the average heights of Species A, B, and C.
Solution:
- Condensed Solution Implementation:
Add the three species' heights for each farm and compare the totals. - Necessary Data points:
Farm W: A=25, B=31, C=44. Farm X: A=28, B=31, C=46. Farm Y: A=26, B=38, C=43. Farm Z: A=27, B=38, C=46. - Calculations Estimations:
W: \(25 + 31 + 44 = 100\). X: \(28 + 31 + 46 = 105\). Y: \(26 + 38 + 43 = 107\). Z: \(27 + 38 + 46 = 111\). - Comparison to Answer Choices:
Farm Z's sum (111) is greater than W (100), X (105), and Y (107).
FINAL ANSWER Blank 1: Z
Question 2: Most Variable Species (Greatest Standard Deviation)
Complete Statement:
For the 3 species, the standard deviation of the 4 average mature heights given on the graph is greatest for Species ______.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: standard deviation of the 4 average mature heights
- Meaning: Standard deviation measures how spread out the values are for each species across the four farms.
- Relation to Chart: Look at how much the heights for each species change from farm to farm.
- Statement Breakdown 2:
- Key Phrase: greatest for Species _____
- Meaning: Identify, for which species — A, B, or C — the heights across the farms are most variable.
- Relation to Chart: Compare the spread for each species across the farms.
- What is needed: Which species (A, B, or C) has the greatest variability in average heights across the four farms.
Solution:
- Condensed Solution Implementation:
Estimate and/or calculate the standard deviations by checking the range and spread for each species. - Necessary Data points:
Species A: 25, 28, 26, 27. Species B: 31, 31, 38, 38. Species C: 44, 46, 43, 46. - Calculations Estimations:
Species B: values split into two clusters (31 and 38), range is 7. Species A and C are closely grouped (range of 3). Standard deviation is higher for B. - Comparison to Answer Choices:
Species B's values are more spread out compared to A and C (which are tightly grouped), so B has the greatest standard deviation.
FINAL ANSWER Blank 2: B
Summary
By adding the heights for each farm, Farm Z has the highest total (111). For the species' variation, Species B's values are split—two at 31, two at 38—making it stand out for the highest standard deviation.
Question Independence Analysis
The two blanks test independent skills: Blank 1 is about total sums across farms, while Blank 2 is about variability within each species. Neither answer is influenced by the other.