The graph shows, for 7 groups—Groups A through G—the relationship between the median and the arithmetic mean of annual salaries...
GMAT Graphics Interpretation : (GI) Questions
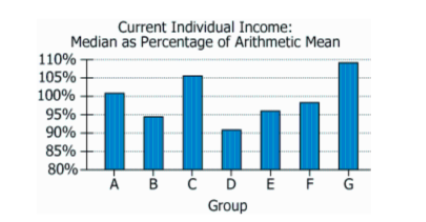
The graph shows, for 7 groups—Groups A through G—the relationship between the median and the arithmetic mean of annual salaries for members of that group. All 7 groups have the same number of employees and each group plans to hire a new worker at the group's median salary.
Based on the information provided, select from each drop-down menu the option that creates the most accurate statement.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Subject | annual salaries for members of that group | Focus is on employee salary data |
| Groups | 7 groups—Groups A through G | There are seven employee groups labeled A to G |
| Metrics Shown | relationship between the median and the arithmetic mean of annual salaries | Shows how the midpoint (median) compares to the average (mean) salary |
| Equal Group Size | All 7 groups have the same number of employees | Each group is equally sized |
| Hiring Plan | Each group plans to hire a new worker at the group's median salary | Each group will add an employee earning exactly the current median salary |
Table 2: Chart Analysis
| Chart Component | What's Displayed | Interpretation |
|---|---|---|
| Y-Axis | 'Median as % of Arithmetic Mean' (80 to 110%) | % above 100 shows median exceeds mean, below 100 means median is less than mean |
| X-Axis | Groups A, B, C, D, E, F, G | Each group compared side-by-side |
| Data | Group A: 101%, B: 94%, C: 106%, D: 91%, E: 96%, F: 98%, G: 109% | Group G: highest (109%), Group D: lowest (91%); A, C, G above 100%, others below |
| Visual Pattern | Bars for A, C, G above 100%; B, D, E, F below 100% | Split between groups where typical salary is above/below average salary (skew direction hint) |
Key Insights
- Groups A, C, and G have median salaries higher than their mean salaries; hiring at the median will increase their mean salary.
- Group G, with the largest gap \(109\%\), will see the greatest percentage rise in mean salary after hiring.
- For Groups B, D, E, and F, where the median is below the mean, hiring at the median salary will decrease their mean salary.
Step-by-Step Solution
Question 1: Number of Groups with Mean Increase
Complete Statement:
For exactly _____ of the groups, the addition of the new worker will result in an increase in the arithmetic mean salary for the group.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: addition of the new worker
- Meaning: Each group hires a new employee.
- Relation to Chart: The new worker is paid at the group's median salary.
- Important Implications: The effect on mean depends on whether the median is greater or less than the mean.
- Statement Breakdown 2:
- Key Phrase: increase in the arithmetic mean salary
- Meaning: The group's average salary rises after adding the new worker.
- Relation to Chart: This increase happens if the median is above the mean \(\mathrm{median/mean} \gt 100\%\).
- Important Implications: Count groups where median as a percentage of mean is over \(100\%\).
- What is needed: The number of groups whose median salary is above their mean salary \(\mathrm{median/mean} \gt 100\%\).
Solution:
- Condensed Solution Implementation:
List each group's median-as-percent-of-mean, then count all above \(100\%\). - Necessary Data points:
Group A: \(101\%\); Group B: \(94\%\); Group C: \(106\%\); Group D: \(91\%\); Group E: \(96\%\); Group F: \(98\%\); Group G: \(109\%\) - Calculations Estimations:
Groups A \((101\%)\), C \((106\%)\), and G \((109\%)\) are all above \(100\%\). That totals 3 groups. - Comparison to Answer Choices:
Of the choices provided (2, 3, 4, 5, 6, 7), '3' matches our count.
FINAL ANSWER Blank 1: 3
Question 2: Group with Greatest Percentage Increase
Complete Statement:
For Group _____, the increase (as a percentage of the previous arithmetic mean) will be the greatest.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: the increase...will be the greatest
- Meaning: Which group will see the largest increase in its average salary.
- Relation to Chart: The group with the highest median/mean percentage will get the largest mean boost after hiring at median.
- Statement Breakdown 2:
- Key Phrase: as a percentage of the previous arithmetic mean
- Meaning: How big the increase is, relative to the group's original mean.
- Relation to Chart: A higher median versus mean percentage leads to a greater relative increase.
- What is needed: The group (with median above mean) that has the highest median/mean percentage.
Solution:
- Condensed Solution Implementation:
From the three groups that increase the mean (A, C, G), select the one with the largest median/mean percentage. - Necessary Data points:
A: \(101\%\); C: \(106\%\); G: \(109\%\) - Calculations Estimations:
\(\mathrm{G}\,(109\%) \gt \mathrm{C}\,(106\%) \gt \mathrm{A}\,(101\%)\), so Group G sees the largest increase. - Comparison to Answer Choices:
Provided choices include 'G', which matches our finding.
FINAL ANSWER Blank 2: G
Summary
Exactly 3 groups (A, C, and G) will see their mean salary increase after hiring a new worker at the median. Among these, Group G will have the greatest percentage increase, due to its median salary being furthest above its mean.
Question Independence Analysis
The questions are dependent: the second uses the set of groups identified as increasing in the first. Both rely on understanding the relationship between median and mean.