The figure represents a boy who is 1.6 m tall standing in front of a lamppost that is 8 m...
GMAT Graphics Interpretation : (GI) Questions
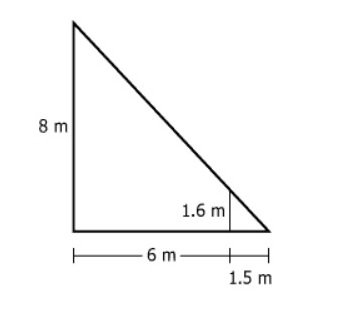
The figure represents a boy who is 1.6 m tall standing in front of a lamppost that is 8 m tall. As shown, the boy casts a shadow that is 1.5 m long when he is 6 m from the lamppost. Note that \(\frac{8}{1.6} = \frac{6+1.5}{1.5}\). As the boy walks in a straight line away from the lamppost, his distance from the lamppost increases and his shadow gets longer. When the boy is 7 m from the lamppost, he casts a shadow that is 1.75 m long.
From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Boy's height | "1.6 m tall" | The boy is 1.6 meters tall |
| Lamppost height | "8 m tall" | The lamppost is 8 meters tall |
| Position 1 | "6 m from the lamppost", "shadow that is 1.5 m long" | At 6 meters from lamppost, the boy's shadow is 1.5 meters long |
| Proportionality check | "\(\frac{8}{1.6} = \frac{6+1.5}{1.5}\)" | The ratio of heights equals the ratio of distances (verifying similarity) |
| Shadow trend | "As the boy...walks away..., his shadow gets longer" | Farther from lamppost, shadow grows longer |
| Position 2 | "7 m from the lamppost", "shadow that is 1.75 m long" | At 7 meters, shadow is 1.75 meters |
Table 2: Chart Analysis
| Chart Component | What It Shows | Interpretation |
|---|---|---|
| Triangle Type | Right triangle diagram | Geometric layout of lamppost, boy, and shadow |
| Vertical side | 8 m | Lamppost height (matches text) |
| Base (horizontal segment) | Two pieces: 6 m (boy's distance), 1.5 m (shadow), total 7.5 m | Boy's distance + shadow length |
| Perpendicular segment | 1.6 m | The boy's height |
| Hypotenuse | Slant from lamppost top through boy to shadow tip | Represents the path of the light |
Key Insights
- The scenario describes two similar right triangles: (1) lamppost-ground-shadow and (2) boy-ground-shadow. This allows us to use proportional reasoning.
- The ratio of lamppost height to boy's height is 5:1 (\(\frac{8}{1.6} = 5\)), so the distance from lamppost to tip of shadow is always 5 times the shadow length.
- The shadow length follows a direct rule: \(\mathrm{shadow\ length} = \frac{\mathrm{boy's\ distance\ from\ lamppost}}{4}\); this relationship is linear and holds for all values observed in the text and image.
Step-by-Step Solution
Question 1: Shadow Length When 8 Meters from the Lamppost
Complete Statement:
When the boy is 8 m from the lamppost, he casts a shadow that is ___ m long.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: When the boy is 8 m from the lamppost
- Meaning: The boy stands 8 meters away from the base of the lamppost.
- Relation to Chart: We are given shadow lengths for 6m and 7m distances in the chart/diagram. The 8m position is a straightforward extension.
- Important Implications: We need to predict the length of the shadow at a greater distance than those explicitly provided.
Statement Breakdown 2:
- Key Phrase: casts a shadow that is ___ m long
- Meaning: Find the exact length of his shadow at this position.
- Relation to Chart: The shadow length directly depends on the distance from the lamppost, forming a consistent pattern as seen in the given data.
- Important Implications: We can use the existing pattern from provided examples to calculate the required value.
What is needed: The length of the boy's shadow when he stands 8 meters from the lamppost.
Solution:
Condensed Solution Implementation:
Use the proportional pattern found in the given examples: shadow length = distance from lamppost divided by 4.
Necessary Data points:
At 6m, shadow = 1.5m (since \(6 \div 4 = 1.5\)). At 7m, shadow = 1.75m (\(7 \div 4 = 1.75\)).
Calculations Estimations:
For 8m: shadow length = \(8 \div 4 = 2\)m.
Comparison to Answer Choices:
Possible answers are 2, 2.25, 2.50, 2.75, 3. The correct value 2m matches the first option.
FINAL ANSWER Blank 1: 2
Question 2: Distance When the Shadow is 3 Meters
Complete Statement:
When the boy casts a shadow that is 3 m long, he is ___ m from the lamppost.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: casts a shadow that is 3 m long
- Meaning: The shadow being cast measures exactly 3 meters.
- Relation to Chart: The provided chart shows shorter shadows (1.5m and 1.75m), so we must extend the pattern.
Statement Breakdown 2:
- Key Phrase: he is ___ m from the lamppost
- Meaning: Find at what distance from the lamppost the boy's shadow measures 3m.
- Relation to Chart: Since shadow = distance ÷ 4, the inverse is distance = shadow × 4.
What is needed: The boy's distance from the lamppost when the shadow is 3 meters long.
Solution:
Condensed Solution Implementation:
Rearrange the proportional rule to solve for distance: distance = shadow length × 4.
Necessary Data points:
Shadow length is given as 3 meters. This follows the same proportional pattern as above.
Calculations Estimations:
Distance = \(3 \times 4 = 12\) meters.
Comparison to Answer Choices:
Possible answers are 9, 10, 11, 12, 13. The correct value 12m matches the fourth option.
FINAL ANSWER Blank 2: 12
Summary
Both blanks are solved using the proportional pattern: shadow length equals distance from lamppost divided by 4. For 8m the shadow is 2m, and for a 3m shadow, the distance is 12m. This predictable relationship allows direct calculation for each scenario.
Question Independence Analysis
The two blanks are independent. The first requires determining the shadow length for a given distance, and the second requires finding the distance for a given shadow length. While both use the same proportional relationship, neither blank's answer depends on the other's result.