The diagram shows the relationships between 3 groups of stockholders of Company HQS and the number of stockholders in each...
GMAT Graphics Interpretation : (GI) Questions
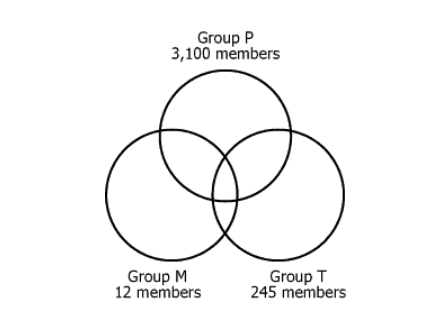
The diagram shows the relationships between 3 groups of stockholders of Company HQS and the number of stockholders in each group
- Group P consists of those stockholders who receive a paper copy of the annual report.
- Group M consists of the majority stockholders.
- Group T consists of those stockholders who are traders
Exactly 8 stockholders belong to all three groups. It is possible that one or more of the regions in the diagram do not contain any members.
Select from each drop-down menu the option that creates the most accurate statement based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Dataset Subject | The diagram shows the relationships between 3 groups of stockholders of Company HQS and the number of stockholders in each group | The diagram displays how Company HQS's stockholders belong to three groups and counts their members |
| Group P Definition | Group P consists of those stockholders who receive a paper copy of the annual report. | Group P includes those who receive a physical annual report |
| Group M Definition | Group M consists of the majority stockholders. | Group M includes those owning a majority of the shares |
| Group T Definition | Group T consists of those stockholders who are traders | Group T is made up of stockholders who trade shares |
| Universal Overlap | Exactly 8 stockholders belong to all three groups. | There are 8 people who are in P, M, and T all at once |
| Empty Region Possible | It is possible that one or more of the regions in the diagram do not contain any members. | Some intersections between groups could have zero members |
Table 2: Chart Analysis
| Chart Component | What's Shown | What This Tells Us |
|---|---|---|
| Chart Type | Venn diagram of 3 overlapping circles | Shows all possible overlaps between groups P, M, T |
| Group P Size | 3,100 members in Group P | Group P is far larger than the other two groups |
| Group M Size | 12 members in Group M | Group M is much smaller than both P and T |
| Group T Size | 245 members in Group T | Group T is significantly larger than M but much smaller than P |
| Three-way Overlap | 8 stockholders in all three groups | Most of Group M also belongs to P and T |
| Overlap Structure | All circles overlap | Every combination of membership is possible (but may be empty) |
Key Insights
The majority stockholders group (M) is the smallest (12 members), with most (8 out of 12) also being in both other groups. The paper report group (P) is overwhelmingly the largest (3,100 members). Only 4 members of M are not in all three groups. This means that any overlap with M is strictly limited to at most 12 people. All regions of the Venn diagram may be empty except the triple intersection (which has 8 members) and the group totals.
Step-by-Step Solution
Question 1: Maximum Traders Receiving Paper Reports
Complete Statement:
If all majority stockholders receive paper reports, then ___ is the maximum number of traders who could receive paper reports.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: all majority stockholders receive paper reports
- Meaning: Every member of the Majority Stockholders group (M) must also be a member of the Paper Report group (P).
- Relation to Chart: All 12 members of M are contained within P in the Venn diagram.
- Important Implications: No majority stockholders are excluded from those receiving paper reports; when maximizing, this enables more overlap.
- Statement Breakdown 2:
- Key Phrase: maximum number of traders who could receive paper reports
- Meaning: We want as many traders (T) as possible to also be paper report recipients (P).
- Relation to Chart: This means maximizing the size of \(\mathrm{T ∩ P}\) by placing as many traders as possible into P, subject to the group constraints.
- Important Implications: The number of traders who receive paper reports cannot exceed the total number of traders (245), and must not violate overlapping group restrictions.
- What is needed: The largest possible value for the intersection \(\mathrm{T ∩ P}\), in other words, the greatest possible number of traders who also receive paper reports.
Solution:
- Condensed Solution Implementation:
All 12 majority stockholders are in P. Of these, 8 are also traders (since exactly 8 people are in all three groups). To maximize \(\mathrm{T ∩ P}\), place all remaining traders \(\mathrm{(245 - 8 = 237)}\) into P, since the size of P (3,100) allows it. - Necessary Data points:
Number of paper recipients (P): 3,100; Number of majority stockholders (M): 12; Number of traders (T): 245; Number of people in all three groups: 8. - Calculations Estimations:
8 traders are in all three groups, so the rest (237 traders) can be placed in P (as P is large enough). Therefore, the maximum is \(\mathrm{8 + 237 = 245}\). - Comparison to Answer Choices:
Of the choices (8, 12, 237, 245), 245 is the maximum and matches our calculation.
FINAL ANSWER Blank 1: 245
Question 2: Maximum Traders Who Are Also Majority Stockholders
Complete Statement:
If exactly 10 majority stockholders receive paper reports, then ___ is the maximum number of traders who could also be majority stockholders.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: exactly 10 majority stockholders receive paper reports
- Meaning: Out of 12 majority stockholders, only 10 are in the Paper Report group (P); 2 majority stockholders are outside P.
- Relation to Chart: \(\mathrm{M ∩ P = 10}\); M has 2 members not in P.
- Statement Breakdown 2:
- Key Phrase: maximum number of traders who could also be majority stockholders
- Meaning: Find the largest possible overlap of members in \(\mathrm{T ∩ M}\), grouping as many majority stockholders into T as possible.
- Relation to Chart: All three group overlap is fixed at 8, so we look for additional \(\mathrm{M ∩ T}\) members who are outside P.
- What is needed: The greatest possible value for the intersection of traders and majority stockholders, \(\mathrm{T ∩ M}\).
Solution:
- Condensed Solution Implementation:
The 8 members in all three groups \(\mathrm{(M ∩ P ∩ T)}\) are part of both M and T. Since only 10 M are in P, there are 2 majority stockholders who are not in P; both can also be in T to maximize \(\mathrm{T ∩ M}\). - Necessary Data points:
Number in all three groups: 8; Number of majority stockholders not in P: 2. - Calculations Estimations:
Maximum is \(\mathrm{8 + 2 = 10}\) (in all three groups + majority stockholder traders not in P). - Comparison to Answer Choices:
Of the choices (0, 2, 8, 10), 10 is the largest possible value and matches our result.
FINAL ANSWER Blank 2: 10
Summary
For both questions, the strategy was to maximize the overlap permitted by the number of members in each group and the required intersections. For Blank 1, all traders can be placed into the paper recipients group, giving 245 as the answer. For Blank 2, the two majority stockholders not in the paper group are added to the 8 in all three groups to maximize trader and majority stockholder overlap, giving 10 as the answer.
Question Independence Analysis
The two questions are independent. Each presents a different constraint regarding the overlap of paper recipients with majority stockholders, and asks about different group overlaps. The solution to one blank does not affect the logic or constraints applied to the other.