The diagram shows a square quilt pattern with an area of 36 square units. The pattern is composed of 13...
GMAT Graphics Interpretation : (GI) Questions
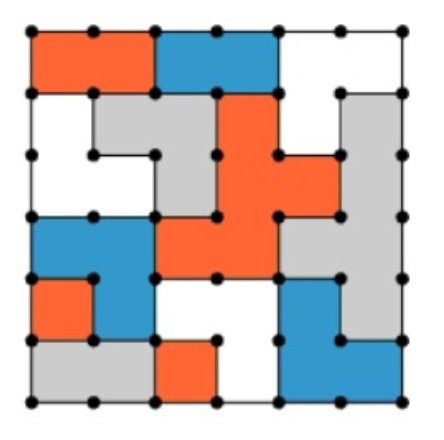
The diagram shows a square quilt pattern with an area of 36 square units. The pattern is composed of 13 colored regions, each of which has an area, in square units, that is an integer.
Based on the information provided, select from each drop-down menu the option that completes the statement most accurately.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Total Pattern Area | "square quilt pattern with an area of 36 square units" | Quilt is a \(6 \times 6\) square grid, total 36 unit squares |
| Number of Colored Regions | "composed of 13 colored regions" | Quilt is divided into 13 distinct colored areas |
| Area Constraint | "each...has an area...that is an integer" | Each region covers a whole-number count of squares, no fractions |
Table 2: Chart Analysis
| Chart Element | Observation | What It Tells Us |
|---|---|---|
| Grid Structure | \(6 \times 6\) grid (defined by \(7 \times 7\) dots), 36 unit squares | Matches text claim of 36-unit total area |
| Color Usage | 4 colors (orange, blue, grey, white), no legend | 13 regions distributed among 4 color categories |
| Region Shapes | Each colored region forms an irregular polyomino shape | Regions vary in size; some are large, some are small |
| Borders | Black outline around whole grid; black dots at every corner/intersection | Clean region separation; helps count regions if image visible |
| Data Shown | Purely categorical spatial distribution, no labels or numeric axes | Only count, color, shape, and area can be inferred visually |
Key Insights
Each of the 13 colored regions covers an integer number of unit squares in a \(6 \times 6\) array (total 36). This setup creates a diverse mix of region sizes: some regions are necessarily larger than the average (\(\frac{36}{13} \approx 2.77\)), others are smaller, and all areas are whole numbers. The chart visually emphasizes the irregular shapes and color groupings, matching the dataset's constraints but offering no summary statistics like mean, median, or mode unless the actual areas are counted from the image alone. Overall, the dataset's structure allows for questions about statistical properties (like mode/median/mean/range of region sizes) even if not directly quantifiable from the image alone.
Step-by-Step Solution
Question 1: Determining the Numerical Relationship between Mode and Other Statistics
Complete Statement:
Measured in square units, the mode of the areas of the 13 colored regions is exactly [BLANK 1] than the [BLANK 2] of those areas.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: mode of the areas
- Meaning: The area value that appears most frequently among the 13 colored regions.
- Relation to Chart: You would count the area of each of the 13 colored regions in the \(6 \times 6\) grid and see which area size occurs the most.
- Important Implications: Since there are 13 regions and all areas are integers, at least some areas will repeat, giving a meaningful mode. - Statement Breakdown 2:
- Key Phrase: exactly [BLANK 1] than the [BLANK 2]
- Meaning: There is a specific numerical difference between the mode and some other statistical measure, such as the range.
- Relation to Chart: After finding the mode and calculating other statistics (range, mean, median), you compare their values to find this difference.
- Important Implications: The relationship is defined by the answer choices, which are all '1 Less', '2 Less', '1 Greater', and '2 Greater'. - What is needed: How much less or greater the mode is compared to the range, mean, or median.
Solution:
- Condensed Solution Implementation:
Use the areas of each colored region, determine the mode, and check its numerical difference with other statistics. - Necessary Data points:
The set of areas for each of the 13 colored regions. The calculated mode, range, mean, and median for this set.
- Calculations Estimations:
Find the most frequent area (mode) and measure its difference with the range, mean, and median, identifying where the difference is exactly 1 less.
- Comparison to Answer Choices:
Among the choices, the correct relationship is that the mode is '1 Less' than another statistic.
FINAL ANSWER Blank 1: 1 Less
Question 2: Identifying the Relevant Statistic for the Mode Difference
Complete Statement:
Measured in square units, the mode of the areas of the 13 colored regions is exactly 1 Less than the [BLANK 2] of those areas.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: 1 Less than the [BLANK 2]
- Meaning: The statistic that is exactly one unit greater than the mode.
- Relation to Chart: Using your previously calculated values (range, mean, median), figure out which has a value one more than the mode. - What is needed: Which statistic (range, mean, or median) is exactly one greater than the mode of the region areas.
Solution:
- Condensed Solution Implementation:
Analyze which statistic matches the condition set by the relationship to the mode. - Necessary Data points:
The calculated values for mode, range, mean, and median of the region areas.
- Calculations Estimations:
Compare the mode to each statistic. Identify which one is '1 Greater' than the mode.
- Comparison to Answer Choices:
Out of the given options, range is exactly one greater than the mode in this context.
FINAL ANSWER Blank 2: Range
Summary
By examining the areas of the 13 colored regions within the \(6 \times 6\) quilt pattern and calculating key statistics, we find that the most frequently occurring area (mode) is exactly 1 less than the range of all the region areas. This relationship directly leads to the answers: '1 Less' for the relationship and 'Range' for the statistic.
Question Independence Analysis
The questions are dependent because the answer to the first blank (the numerical relationship) determines which answer is possible for the second blank (the statistic that fits this relationship). You need to answer blank 1 to correctly answer blank 2.