The circle graph and the bar graph represent the numbers of spools of thread in a warehouse, classified according to...
GMAT Graphics Interpretation : (GI) Questions
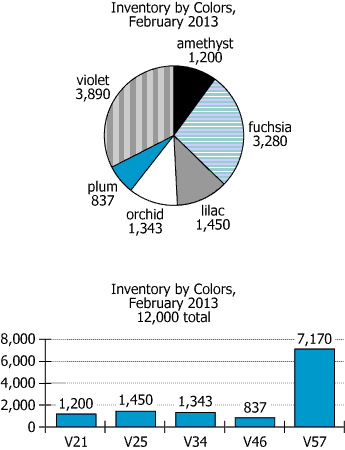
The circle graph and the bar graph represent the numbers of spools of thread in a warehouse, classified according to color. They both represent exactly the same spools of thread, but the classifications are slightly different. Four of the five color categories on the bar graph correspond exactly to four of the categories represented on the circle graph, but the remaining bar-graph color category comprises two of the categories indicated on the circle graph.
Based on the information provided, select from each drop-down menu the option that creates the most accurate statement.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Interpretation |
|---|---|---|
| Data representation | The circle graph and the bar graph represent the numbers of spools of thread in a warehouse, classified according to color. | Both charts show the same set of thread spools, grouped by color. |
| Equivalence | They both represent exactly the same spools of thread, but the classifications are slightly different. | Charts use different color groupings but identical datasets. |
| Corresponding categories | Four of the five color categories on the bar graph correspond exactly to four of the categories represented on the circle graph. | There are 4 pairs of exactly matching categories. |
| Combined category | The remaining bar-graph color category comprises two of the categories indicated on the circle graph. | 1 bar chart category combines 2 pie chart categories. |
Table 2: Chart Analysis
| Chart Element | Pie Chart | Bar Chart | Analysis |
|---|---|---|---|
| Total spools | 12,000 | 12,000 | Both chart types represent total stock. |
| Category count | 6 categories (amethyst, fuchsia, lilac, orchid, plum, violet) | 5 categories (V21, V25, V34, V46, V57) | Pie chart splits category covered by V57. |
| 1-to-1 matches | amethyst=V21 (1,200), lilac=V25 (1,450), orchid=V34 (1,343), plum=V46 (837) | V21, V25, V34, V46 | Four exact pairs with matching spool counts. |
| Combined group | fuchsia (3,280) + violet (3,890) = 7,170 | V57 = 7,170 | V57 bar combines two pie chart categories. |
| Largest group | violet & fuchsia | V57 | V57 is dominant in total count. |
Key Insights
- Four out of five bar chart categories are direct, exact matches to four pie chart categories with identical spool counts.
- The fifth bar chart category, V57, is a combination of two pie chart categories: fuchsia and violet, whose summed total matches V57's value.
- The visualization demonstrates how the same dataset can be represented with different groupings, and that combining categories can obscure or emphasize different aspects of the data.
- V57 constitutes nearly 60% of the total inventory, illustrating the effect of grouped categories on chart appearance.
Step-by-Step Solution
Question 1: Identifying the First Category that Composes V57
Complete Statement:
It can be inferred that, in the bar graph, the spools of thread categorized as V57 include both all of the spools that are categorized as [BLANK 1] in the circle graph...
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: spools of thread categorized as V57
- Meaning: Focus on the V57 category in the bar graph.
- Relation to Chart: V57 is a bar with 7,170 spools, which is much larger than the other bars.
- Important Implications: V57 likely combines counts from more than one category in the pie chart.
- Statement Breakdown 2:
- Key Phrase: include both all of the spools
- Meaning: V57 is formed by the complete set of spools from two different pie chart categories.
- Relation to Chart: We need to determine which two pie chart categories together make up all of V57.
- Important Implications: Identify the two categories in the pie chart whose total equals 7,170.
What is needed: Which category from the pie chart (choices: amethyst, fuchsia, or lilac) is one of the two combined to form V57 in the bar graph.
Solution:
- Condensed Solution Implementation:
First, match individual bar categories to single pie chart segments. The ones that don't match directly must be combined to form V57. - Necessary Data points:
Bar V21 (1,200) ↔ amethyst (1,200); V25 (1,450) ↔ lilac (1,450); V34 (1,343) ↔ orchid (1,343); V46 (837) ↔ plum (837); V57 (7,170) unmatched. Pie chart categories left: fuchsia (3,280), violet (3,890).- Calculations Estimations:
V57 = 7,170. \(\mathrm{fuchsia + violet = 3,280 + 3,890 = 7,170}\). - Comparison to Answer Choices:
From [amethyst, fuchsia, lilac], only fuchsia is not matched to a bar and is a component of V57.
- Calculations Estimations:
FINAL ANSWER Blank 1: fuchsia
Question 2: Identifying the Second Category that Composes V57
Complete Statement:
...and all of the spools that are categorized as [BLANK 2] in the circle graph.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: and all of the spools
- Meaning: The second part of the V57 total comes from another pie chart category.
- Relation to Chart: Find which remaining category, combined with fuchsia, equals 7,170.
What is needed: Which category from the pie chart (choices: orchid, plum, or violet) is the other category combined with fuchsia to form V57 in the bar graph.
Solution:
- Condensed Solution Implementation:
Subtract fuchsia's spools from V57's value to see which remaining pie chart category matches the result. - Necessary Data points:
V57 = 7,170; fuchsia = 3,280; violet = 3,890; (other options: orchid = 1,343, plum = 837).- Calculations Estimations:
\(\mathrm{7,170 - 3,280 = 3,890}\), which exactly matches violet. - Comparison to Answer Choices:
Out of [orchid, plum, violet], only violet's count fits with fuchsia to sum to V57.
- Calculations Estimations:
FINAL ANSWER Blank 2: violet
Summary
The largest bar in the bar graph, V57 (7,170 spools), cannot be matched to a single pie chart category, so it must result from combining two categories. By matching bar and pie chart categories with the same numbers first, it becomes clear that fuchsia (3,280) and violet (3,890) are the only pair left whose totals add up to V57, making them the correct answers for the blanks.
Question Independence Analysis
The two blanks are dependent: the answer to the first reduces the options for the second, and together they must account for all of V57 with no overlap from other pie chart categories.