Test audiences screened five 3-minute previews of a certain movie. The movie contains both drama and comedy, but the previews...
GMAT Graphics Interpretation : (GI) Questions
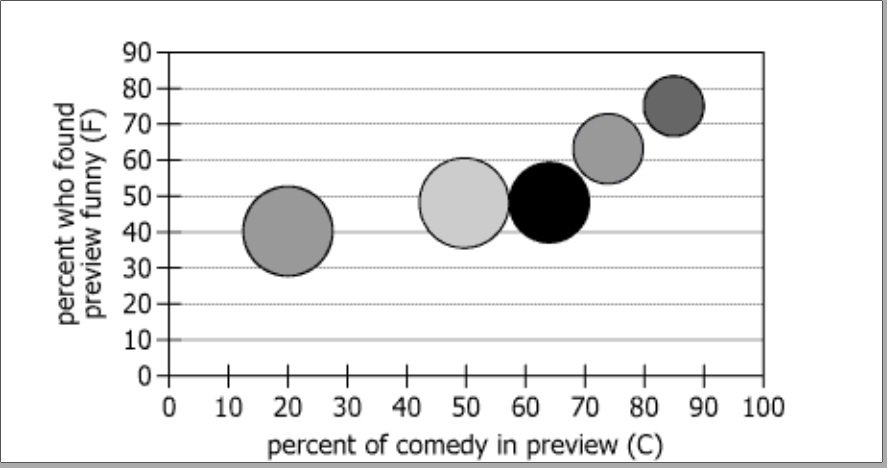
Test audiences screened five 3-minute previews of a certain movie. The movie contains both drama and comedy, but the previews were customized to show differing percentages of comedic and dramatic scenes (measured by screen time). The test audiences were asked, Do you think the preview is funny? and How likely are you to see the movie on the weekend it opens? The position of the center of each bubble indicates the percent of comedy (C) in the previews and the percent of test audience members who found the previews funny (F), and the greater the bubble's size the greater the average reported likelihood (L) of their seeing the movie on the opening weekend.
Select the option from each drop-down menu that creates the most accurate statement on the basis of the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Interpretation |
|---|---|---|
| Study setup | Test audiences screened five 3-minute previews of a certain movie | 5 unique previews shown to test audiences |
| Movie content | The movie contains both drama and comedy | The main film mixes drama and comedy genres |
| Preview customization | Previews were customized to show differing percentages of comedic and dramatic scenes (measured by screen time) | Each preview had a different proportion of comedy and drama |
| Audience question 1 | Do you think the preview is funny? | Audiences judged if the preview was funny |
| Audience question 2 | How likely are you to see the movie on the weekend it opens? | Audiences indicated likelihood to see main film |
| X-axis meaning | The position of the center of each bubble indicates the percent of comedy (\(\mathrm{C}\)) in the previews | Horizontal bubble position = comedy percent in preview |
| Y-axis meaning | ...and the percent of test audience members who found the previews funny (\(\mathrm{F}\)) | Vertical bubble position = percent finding it funny |
| Bubble size meaning | ...the greater the bubble's size the greater the average reported likelihood (\(\mathrm{L}\)) of their seeing the movie on the opening weekend | Bubble size = audience's average likelihood to see movie |
Table 2: Chart Analysis
| Chart Element | Description | Interpretation |
|---|---|---|
| Chart Type | Bubble scatter plot; 5 bubbles | Each bubble = 1 unique preview mix |
| X-axis | Percent of comedy (\(\mathrm{C}\)) in preview, ranging ~20% to ~92% | Varies from mostly dramatic to highly comedic |
| Y-axis | Percent of audience finding preview funny (\(\mathrm{F}\)), ranging ~37% to ~78% | More comedy, more people find it funny |
| Bubble Size | Size proportional to average likelihood (\(\mathrm{L}\)) of seeing the movie | Shows which preview mix drives highest interest |
| Trend | Bubbles ascend from lower left to upper right | Strong positive relationship between \(\mathrm{C}\) and \(\mathrm{F}\) |
| Biggest Bubble | Around 55% comedy | Audience most eager when preview is balanced |
| Data Spread | Bubble sizes vary; not all largest at highest \(\mathrm{C}\) or lowest \(\mathrm{C}\) | Peak interest not at extremes, but in middle |
Key Insights
- A higher percentage of comedy in the preview (\(\mathrm{C}\)) strongly increases the percent of audience members who find it funny (\(\mathrm{F}\)), showing a clear positive correlation between \(\mathrm{C}\) and \(\mathrm{F}\).
- The highest reported likelihood to see the movie (\(\mathrm{L}\)) is at a moderate, not extreme, comedy level, suggesting audience interest peaks with a mix of comedy and drama.
- Increasing drama necessarily reduces comedy (since \(\mathrm{C + D = 100}\)), so drama percentage (\(\mathrm{D}\)) negatively correlates with \(\mathrm{F}\) and with anticipated movie attendance.
Step-by-Step Solution
Question 1: Variables That Could Differ with Different Audiences
Complete Statement:
If the same previews were shown to other test audiences, ______ could differ from the results shown.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: same previews
Meaning: Refers to using the identical 3-minute preview videos as were previously tested.
Relation to Chart: Each bubble represents a specific preview's fixed content on the chart.
Important Implications: The percentage of comedy (\(\mathrm{C}\)) in each preview does not change regardless of audience.
- Key Phrase: same previews
- Statement Breakdown 2:
- Key Phrase: other test audiences
Meaning: Refers to different groups of people watching the same previews.
Relation to Chart: Current chart is based on one audience; a new audience might produce different results.
Important Implications: Variables reliant on opinions or preferences could differ between audiences.
- Key Phrase: other test audiences
- What is needed: Which variables shown (\(\mathrm{C}\), \(\mathrm{F}\), and \(\mathrm{L}\)) might change if different audiences were shown the same previews.
Solution:
- Condensed Solution Implementation:
Identify which variables are inherent to the previews (fixed) versus those dependent on audience opinions (variable). - Necessary Data points:
\(\mathrm{C}\) = percent comedy (fixed by preview content), \(\mathrm{F}\) = percent who found preview funny (audience-dependent), \(\mathrm{L}\) = likelihood to see movie (audience-dependent).- Calculations Estimations:
No calculation required; logical classification between fixed content and audience response. - Comparison to Answer Choices:
\(\mathrm{C}\) does not change. \(\mathrm{F}\) and \(\mathrm{L}\) would change with a different audience. Therefore, only \(\mathrm{F}\) and \(\mathrm{L}\) could differ.
- Calculations Estimations:
FINAL ANSWER Blank 1: only F and L
Question 2: Correlation Between Drama Percentage and 'Finding Funny' Percent
Complete Statement:
Let \(\mathrm{D}\) equal the percent of drama in each preview. Assuming each preview is made up entirely of comedy and drama (such that \(\mathrm{C + D = 100}\)), there is ______ correlation between \(\mathrm{D}\) and \(\mathrm{F}\).
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: D equal the percent of drama
Meaning: \(\mathrm{D}\) is defined as the percent of dramatic content in each preview.
Relation to Chart: \(\mathrm{D}\) does not appear on the chart but can be calculated as \(\mathrm{D = 100 - C}\).
- Key Phrase: D equal the percent of drama
- Statement Breakdown 2:
- Key Phrase: C + D = 100
Meaning: Previews are made only of comedy and drama; their percentages sum to 100%.
Relation to Chart: If \(\mathrm{C}\) is given for a bubble, \(\mathrm{D}\) is determined automatically.
- Key Phrase: C + D = 100
- What is needed: Whether the correlation between percent drama (\(\mathrm{D}\)) and percentage finding it funny (\(\mathrm{F}\)) is positive, negative, or none.
Solution:
- Condensed Solution Implementation:
Since \(\mathrm{D = 100 - C}\), increasing \(\mathrm{D}\) means decreasing \(\mathrm{C}\). The chart shows that as \(\mathrm{C}\) (comedy) increases, \(\mathrm{F}\) (funny) increases. Therefore, as \(\mathrm{D}\) increases, \(\mathrm{F}\) decreases. - Necessary Data points:
Positive correlation exists between \(\mathrm{C}\) and \(\mathrm{F}\); \(\mathrm{D}\) is the complement of \(\mathrm{C}\).- Calculations Estimations:
As \(\mathrm{D}\) rises (\(\mathrm{C}\) falls), \(\mathrm{F}\) falls (since higher comedy leads to higher funny percentage). Thus, negative correlation. - Comparison to Answer Choices:
Since \(\mathrm{F}\) decreases as \(\mathrm{D}\) increases (opposite directions), this is a negative correlation.
- Calculations Estimations:
FINAL ANSWER Blank 2: a negative
Summary
For Blank 1, only audience-dependent variables (\(\mathrm{F}\) and \(\mathrm{L}\)) could differ with new audiences; \(\mathrm{C}\) is determined by preview content. For Blank 2, since \(\mathrm{D}\) increases as \(\mathrm{C}\) decreases, and \(\mathrm{C}\) has a positive relationship with \(\mathrm{F}\), \(\mathrm{D}\) and \(\mathrm{F}\) are negatively correlated.
Question Independence Analysis
Both blanks are independent. The first targets variable dependence on audience, while the second addresses mathematical correlation; neither answer depends on the other.