Substance X is an ingredient in over 400 commercially available food products. The graph shows the per-serving amount of Substance...
GMAT Graphics Interpretation : (GI) Questions
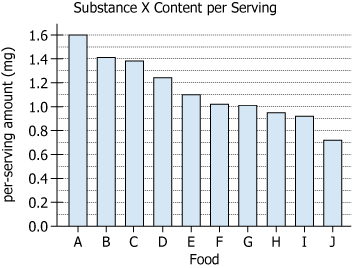
Substance X is an ingredient in over 400 commercially available food products. The graph shows the per-serving amount of Substance X, in milligrams (mg), for each of the 10 commercially available food products—Foods A through J—that have the greatest per-serving amount of Substance X. Based on the information provided, select from each drop-down menu the option that creates the most accurate statement.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Substance X presence | Substance X is an ingredient in over 400 commercially available food products. | Substance X can be found in more than 400 foods you can buy. |
| Graph context | The graph shows the per-serving amount of Substance X, in milligrams (mg), for each of the 10 commercially available food products—Foods A through J—that have the greatest per-serving amount of Substance X. | The chart displays how much Substance X is in one serving of each of the 10 foods (A–J) with the highest amounts. |
Table 2: Chart Analysis
| Chart Component | What's Shown | What This Tells Us |
|---|---|---|
| Chart Type | Vertical bar graph with 10 bars | Shows comparative Substance X content across foods A–J |
| X-Axis | Foods labeled A through J | These are the top 10 foods with most Substance X per serving |
| Y-Axis | Amount of Substance X per serving in milligrams (mg), scale from 0 up to \(1.6\) | Enables reading actual per-serving amounts for each food |
| Pattern | Bar heights decrease from A (\(1.6\) mg) to J (\(0.76\) mg) | Foods are ordered from highest to lowest Substance X content per serving |
| Value Range | Food A: \(1.6\) mg, Food J: \(0.76\) mg | More than a twofold difference between highest and lowest among these ten items |
Key Insights
- Among over 400 foods containing Substance X, the 10 with the greatest amounts range from \(1.6\) mg (Food A) to \(0.76\) mg (Food J) per serving.
- The top item (Food A) has more than twice as much Substance X as the lowest in the top ten (Food J).
- Even among just the highest-content foods, there is significant variation in Substance X per serving.
- The data only covers the top 10 foods, so nothing can be concluded about the average or distribution for all 400+ products.
Step-by-Step Solution
Question 1: Median of Top 10 Foods
Complete Statement:
For the 10 foods in the graph, the median per-serving amount of Substance X is [BLANK] \(1.1\) mg.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: 10 foods in the graph
- Meaning: We are only considering the 10 foods labeled A through J depicted in the chart.
- Relation to Chart: These foods are displayed in order of decreasing Substance X content per serving.
- Important Implications: Our dataset for this question is just these specific 10 values.
Statement Breakdown 2:
- Key Phrase: median per-serving amount
- Meaning: The middle value when the 10 amounts are sorted in order.
- Relation to Chart: Since there are 10 foods, the median is the average of the 5th and 6th highest values.
- Important Implications: We need to identify foods in the 5th and 6th positions and calculate their average.
What is needed: We need to establish the relationship (less than, equal to, or greater than) between the median of the 10 values and \(1.1\) mg.
Solution:
Condensed Solution Implementation:
Order the 10 values and take the average of the 5th and 6th numbers to get the median; then compare that result to \(1.1\) mg.
Necessary Data points:
Food E (5th) = \(1.1\) mg; Food F (6th) = \(1.02\) mg.
Calculations Estimations:
Median = \(\frac{1.1 + 1.02}{2} = 1.06\) mg.
Comparison to Answer Choices:
\(1.06\) mg is less than \(1.1\) mg.
FINAL ANSWER Blank 1: less than
Question 2: Average for All 400+ Foods
Complete Statement:
For all commercially available foods that contain Substance X, the average (arithmetic mean) per-serving amount of Substance X is [BLANK] \(0.8\) mg.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: all commercially available foods
- Meaning: This includes not just the 10 shown, but over 400 foods in total.
- Relation to Chart: Chart shows only the top 10; the rest have even lower amounts.
Statement Breakdown 2:
- Key Phrase: average (arithmetic mean) per-serving amount
- Meaning: Add up all per-serving amounts from all 400+ foods and divide by the total number.
- Relation to Chart: Because the highest 10 values already average close to 1 mg and all remaining foods have lower values, the total average is pulled down.
What is needed: Does the overall average for all 400+ foods exceed, equal, or fall below \(0.8\) mg?
Solution:
Condensed Solution Implementation:
Infer by noting that the 10th highest value is \(0.76\) mg, so all 390+ additional foods have values at or less than \(0.76\) mg, lowering the overall average.
Necessary Data points:
Top 10 values: \(1.6\) to \(0.76\) mg. Remaining 390+ foods: each ≤ \(0.76\) mg.
Calculations Estimations:
Even if all additional foods have exactly \(0.76\) mg, the average is pulled below that by the sheer number of values at/below that level, and many are likely much lower.
Comparison to Answer Choices:
The average for all 400+ foods is less than \(0.8\) mg.
FINAL ANSWER Blank 2: less than
Summary
For blank 1, the median of the 10 shown foods is \(1.06\) mg, which is less than \(1.1\) mg. For blank 2, since only the top 10 foods are above \(0.76\) mg and the other 390+ have ≤ \(0.76\) mg, the mean for all 400+ foods is also less than \(0.8\) mg.
Question Independence Analysis
Question 1 and Question 2 are independent: the first is about the median of a small, specific group (top 10 foods), while the second concerns the overall mean of a much larger set (all 400+ foods). Solving one does not require, nor does it affect, the answer to the other.