On the number line shown, is zero halfway between r and s? s is to the right of zero The...
GMAT Data Sufficiency : (DS) Questions
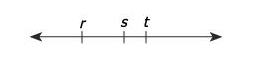
On the number line shown, is zero halfway between \(\mathrm{r}\) and \(\mathrm{s}\)?
- \(\mathrm{s}\) is to the right of zero
- The distance between \(\mathrm{t}\) and \(\mathrm{r}\) is the same as the distance between \(\mathrm{t}\) and \(\mathrm{-s}\)
Understanding the Question
We need to determine whether zero is halfway between r and s on a number line.
For zero to be halfway between two points, those points must be equidistant from zero but on opposite sides. This means one point must be the negative of the other (like -3 and +3).
In mathematical terms, we're asking: Is \(\mathrm{r + s = 0}\)? Or equivalently: Is \(\mathrm{s = -r}\)?
This is a yes/no question. We need sufficient information to answer definitively YES (if \(\mathrm{r + s = 0}\)) or NO (if \(\mathrm{r + s ≠ 0}\)).
Important: The diagram shows us that \(\mathrm{r < s < t}\). While we cannot trust the scale or exact distances in GMAT diagrams, we can trust the relative ordering of points as labeled. This constraint must be respected in all our examples.
Analyzing Statement 1
Statement 1: s is to the right of zero (\(\mathrm{s > 0}\)).
This tells us s is positive, but we know nothing about where r is located.
Let's test different scenarios that respect \(\mathrm{r < s < t}\):
- Case 1: If \(\mathrm{r = -5}\), \(\mathrm{s = 5}\), \(\mathrm{t = 10}\), then \(\mathrm{r + s = 0}\) → YES, zero is halfway between them
- Case 2: If \(\mathrm{r = -3}\), \(\mathrm{s = 5}\), \(\mathrm{t = 10}\), then \(\mathrm{r + s = 2 ≠ 0}\) → NO, zero is not halfway between them
Since we can get both YES and NO answers depending on where r is placed, Statement 1 is NOT sufficient.
[STOP - Not Sufficient!] This eliminates choices A and D.
Analyzing Statement 2
Important: We now forget Statement 1 completely and analyze Statement 2 independently.
Statement 2: The distance between t and r equals the distance between t and -s.
Mathematically: \(\mathrm{|t - r| = |t - (-s)| = |t + s|}\)
From the diagram, we know \(\mathrm{r < s < t}\), which means \(\mathrm{t > r}\). Therefore:
- \(\mathrm{|t - r| = t - r}\) (since t > r)
So our equation becomes: \(\mathrm{t - r = |t + s|}\)
The absolute value \(\mathrm{|t + s|}\) creates two possible cases:
Case 1: If \(\mathrm{t + s ≥ 0}\), then \(\mathrm{|t + s| = t + s}\)
- \(\mathrm{t - r = t + s}\)
- \(\mathrm{-r = s}\)
- \(\mathrm{r = -s}\) → This means \(\mathrm{r + s = 0}\) → YES answer
Case 2: If \(\mathrm{t + s < 0}\), then \(\mathrm{|t + s| = -(t + s)}\)
- \(\mathrm{t - r = -t - s}\)
- \(\mathrm{2t = r - s}\)
- This does NOT tell us whether \(\mathrm{r + s = 0}\) → Could be YES or NO
Let's verify with concrete examples that respect \(\mathrm{r < s < t}\):
Example 1: \(\mathrm{r = -4, s = 4, t = 4}\)
- Check ordering: \(\mathrm{-4 < 4 < 4}\) ✗ (t is not strictly greater than s)
- Let's use: \(\mathrm{r = -5, s = 3, t = 4}\)
- Check ordering: \(\mathrm{-5 < 3 < 4}\) ✓
- Statement 2: \(\mathrm{|4 - (-5)| = 9}\) and \(\mathrm{|4 - (-3)| = 7}\) ✗
- Let's use: \(\mathrm{r = -3, s = 3, t = 3}\)
- Check ordering: \(\mathrm{-3 < 3 < 3}\) ✗
Example that works: \(\mathrm{r = -10, s = -5, t = -2.5}\)
- Check ordering: \(\mathrm{-10 < -5 < -2.5}\) ✓
- Statement 2: Distance from t to r: \(\mathrm{|-2.5 - (-10)| = 7.5}\)
- Distance from t to -s: \(\mathrm{|-2.5 - 5| = 7.5}\) ✓
- Question: \(\mathrm{r + s = -10 + (-5) = -15 ≠ 0}\) → NO answer
Another example: \(\mathrm{r = -5, s = 5, t = 5.01}\)
- Check ordering: \(\mathrm{-5 < 5 < 5.01}\) ✓
- Statement 2: Distance from t to r: \(\mathrm{|5.01 - (-5)| ≈ 10.01}\)
- Distance from t to -s: \(\mathrm{|5.01 - (-5)| = 10.01}\) ✓
- Question: \(\mathrm{r + s = 0}\) → YES answer
Since we can construct valid examples giving both YES and NO answers, Statement 2 is NOT sufficient.
[STOP - Not Sufficient!] This eliminates choice B.
Combining Statements
Now we use both statements together:
- From Statement 1: \(\mathrm{s > 0}\) (s is positive)
- From Statement 2: \(\mathrm{t - r = |t + s|}\)
- From the diagram: \(\mathrm{r < s < t}\)
Key insight: Since \(\mathrm{s > 0}\) (Statement 1) and \(\mathrm{t > s}\) (from diagram), we know:
- \(\mathrm{t > s > 0}\)
- Therefore, both t and s are positive
- This means \(\mathrm{t + s > 0}\)
Since \(\mathrm{t + s > 0}\), we are in Case 1 from our Statement 2 analysis:
- \(\mathrm{|t + s| = t + s}\)
- \(\mathrm{t - r = t + s}\)
- \(\mathrm{-r = s}\)
- \(\mathrm{r = -s}\)
- Therefore: \(\mathrm{r + s = 0}\) ✓
Let's verify we cannot construct a counterexample that satisfies both statements:
Test: Can we find values where \(\mathrm{r < s < t}\), \(\mathrm{s > 0}\), \(\mathrm{t - r = |t + s|}\), but \(\mathrm{r + s ≠ 0}\)?
From Statement 1, \(\mathrm{s > 0}\). From the diagram, \(\mathrm{t > s}\), so \(\mathrm{t > 0}\). This forces \(\mathrm{t + s > 0}\), which forces \(\mathrm{r = -s}\).
There is no way to satisfy both statements without having \(\mathrm{r + s = 0}\).
Therefore, the statements together ARE sufficient to answer the question with a definitive YES.
[SUFFICIENT!]
The Answer: C
Statement 1 alone is not sufficient. Statement 2 alone is not sufficient. But both statements together ARE sufficient to determine that zero is halfway between r and s.
Answer Choice C: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.