In the figure above, is the area of triangular region ABC equal to the area of triangular region DBA ?...
GMAT Data Sufficiency : (DS) Questions
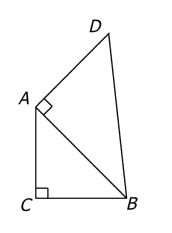
In the figure above, is the area of triangular region ABC equal to the area of triangular region DBA ?
- \(\mathrm{(AC)}^2=2\mathrm{(AD)}^2\)
- \(\triangle\mathrm{ABC}\) is isosceles.
Understanding the Question
We need to determine whether the area of triangle ABC equals the area of triangle DBA.
Given Information
- AC is vertical, CB is horizontal, with \(\angle \mathrm{ACB} = 90°\)
- \(\mathrm{AD} \perp \mathrm{AB}\) (perpendicular at point A)
- Both triangles share side AB
Key Insight for Area Comparison
Since both triangles share the same base AB, they will have equal areas if and only if they have equal heights (perpendicular distances from C and D to line AB).
Therefore, our question becomes: Is the height from C to line AB equal to the height from D to line AB?
Note: The height from D to AB is simply |AD| since \(\mathrm{AD} \perp \mathrm{AB}\).
Analyzing Statement 1
Statement 1: \((\mathrm{AC})^2 = 2(\mathrm{AD})^2\)
This tells us that \(\mathrm{AC} = \sqrt{2} \cdot \mathrm{AD}\).
What This Gives Us
We now know the exact relationship between AC and AD.
What We Still Need
However, we don't know:
- The length of BC
- Where exactly point B is located (other than being on the horizontal line through C)
- How the height from C to AB relates to AD
Testing Different Scenarios
Scenario 1: If BC is relatively short
- Triangle ABC becomes "tall and narrow"
- The height from C to AB will be relatively small
- This height could be less than AD
Scenario 2: If BC is longer
- Triangle ABC becomes more "spread out"
- The height from C to AB increases
- This height could equal or exceed AD
Since we can construct triangles with \(\mathrm{AC} = \sqrt{2} \cdot \mathrm{AD}\) but different values of BC, we get different heights from C to AB. This means different area relationships are possible.
Conclusion for Statement 1
Statement 1 is NOT sufficient because knowing \(\mathrm{AC} = \sqrt{2} \cdot \mathrm{AD}\) doesn't determine the height from C to AB.
[STOP - Not Sufficient!] This eliminates choices A and D.
Analyzing Statement 2
Now we analyze Statement 2 independently, forgetting Statement 1 completely.
Statement 2: Triangle ABC is isosceles
This means two sides of triangle ABC are equal.
What This Gives Us
Three possibilities exist:
- AC = BC (making a right isosceles triangle)
- AC = AB
- BC = AB
Why This Isn't Enough
Without knowing:
- Which sides are equal
- Any specific lengths
- Any relationship to triangle DBA or AD
We cannot determine if the areas match. For example:
- If AC = BC = 1 and AD happens to equal \(1/\sqrt{2}\), the areas might be equal
- If AC = BC = 1 and AD = 2, the areas would definitely differ
- Different isosceles configurations give different area relationships
Conclusion for Statement 2
Statement 2 is NOT sufficient because it tells us nothing about the relationship between triangles ABC and DBA.
[STOP - Not Sufficient!] This eliminates choice B (and confirms D is already eliminated).
Combining Both Statements
Combined Information
From both statements together:
- \(\mathrm{AC} = \sqrt{2} \cdot \mathrm{AD}\) (from Statement 1)
- Triangle ABC is isosceles (from Statement 2)
- \(\mathrm{AC} \perp \mathrm{CB}\) (given in the figure)
The Key Deduction
With \(\mathrm{AC} \perp \mathrm{CB}\) and triangle ABC being isosceles, let's determine which configuration is geometrically possible:
- If AC = AB: In a right triangle, this would mean a leg equals the hypotenuse. Impossible!
- If BC = AB: In a right triangle, this would mean a leg equals the hypotenuse. Impossible!
- Therefore, we must have AC = BC
This makes triangle ABC a 45-45-90 right isosceles triangle.
Finding the Heights
For a 45-45-90 triangle with legs AC = BC:
- The height from C to the hypotenuse AB equals \(\mathrm{AC}/\sqrt{2}\)
- This is a standard property of right isosceles triangles
Now, using Statement 1:
- Height from C to AB = \(\mathrm{AC}/\sqrt{2} = (\sqrt{2} \cdot \mathrm{AD})/\sqrt{2} = \mathrm{AD}\)
- Height from D to AB = AD (given that \(\mathrm{AD} \perp \mathrm{AB}\))
The Answer to Our Question
Since both heights equal AD:
- Same base (AB) + Same height (AD) = Equal areas
[STOP - Sufficient!] We've established the areas must be equal.
The Answer: C
Both statements together are sufficient because they uniquely determine that:
- Triangle ABC must be right isosceles with AC = BC
- This configuration, combined with \(\mathrm{AC} = \sqrt{2} \cdot \mathrm{AD}\), makes both triangular areas equal
Neither statement alone provides enough information to answer the question.
Answer Choice C: "Both statements together are sufficient, but neither statement alone is sufficient.