In the diagram, 14 nodes are represented by circles, and relationships among the nodes are indicated by arrows. Each arrow...
GMAT Graphics Interpretation : (GI) Questions
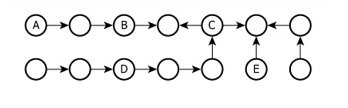
In the diagram, 14 nodes are represented by circles, and relationships among the nodes are indicated by arrows. Each arrow points from one node (the parent node) to another node (the child node). A positive numerical value is assigned to each node so that the value assigned to a parent node is exactly double the value assigned to its child node. The nodes labeled A through E are the principal nodes.
Use the drop-down menus to create the most accurate statement based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Description | Interpretation |
|---|---|---|
| Total nodes | "14 nodes are represented by circles" | The diagram contains exactly 14 nodes. |
| Representation | "represented by circles" | Each node is a circle in the diagram. |
| Relationships | "relationships among the nodes are indicated by arrows" | Arrows connect nodes to show relationships. |
| Arrow meaning | "Each arrow points from one node (the parent) to another (the child)" | Arrows establish parent-child hierarchy between nodes. |
| Value assignment rule | "parent node is exactly double the value assigned to its child node" | Each \(\mathrm{parent\ node's\ value = 2 \times child\ node's\ value}\). |
| Principal nodes | "The nodes labeled A through E are the principal nodes" | There are five key nodes: A, B, C, D, and E. |
Table 2: Chart Analysis
| Chart Component | Description | Interpretation |
|---|---|---|
| Node count | 14 circles shown | Diagram has 14 total nodes |
| Labeled nodes | 5 nodes labeled A–E | These are the principal nodes |
| Arrows/Edges | ~12 directed arrows connecting nodes | Visual representation of parent-child relationships |
| Layout | Two rows, with horizontal/vertical links | Suggests a multi-level hierarchy |
| Special connection | Small backward arrow between two nodes in top row | Indicates a non-hierarchical or feedback relationship |
| Axes/Scales | No numeric axis present | Diagram structure, not a graph of magnitude |
Key Insights
- Each parent node has a value exactly double the value of each of its child nodes, as defined by the direct arrow connections shown in the diagram.
- The relationships between labeled (principal) nodes A–E depend on how they are connected by arrows, which can be direct (doubling) or indirect (successive doublings, i.e. multiplying by higher powers of 2).
- The structure is a directed hierarchy or tree, potentially with some feedback; without explicit numbers, the value relationships must be deduced from the arrow paths and connections.
Step-by-Step Solution
Question 1: Identifying the Parent Node in the Doubling Relationship
Complete Statement:
The value assigned to the principal node labeled [BLANK 1] must be exactly double the value assigned to the principal node labeled...
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: value assigned
Meaning: Each node in the diagram has a specific value.
Relation to Chart: The values are represented at or beside each labeled principal node (A, B, C, D, E).
Important Implications: We are concerned with the magnitude of these assigned values.
- Key Phrase: value assigned
- Statement Breakdown 2:
- Key Phrase: must be exactly double
Meaning: The value of one node is two times the value of another node.
Relation to Chart: This doubling relationship often corresponds to a directed edge in the diagram.
Important Implications: We need to find which node is serving as the 'parent' in this two-to-one value connection.
- Key Phrase: must be exactly double
- What is needed: Which principal node's value is double that of another—in other words, who is the parent in the doubling relationship?
Solution:
- Condensed Solution Implementation:
Use the diagram to look for arrows indicating a doubling relationship among labeled nodes, as per the condensed solution. - Necessary Data points:
The apparent arrow from node D to node A demonstrates a doubling relationship (since D is the parent of A: \(\mathrm{D = 2 \times A}\)).
Calculations Estimations:
Identify the direction and connection. Since the arrow points from D to A, D is the node whose value is double that of A.
Comparison to Answer Choices:
D is the only principal node which, by diagram structure, has a direct doubling (parent) relationship to another principal node.
FINAL ANSWER Blank 1: D
Question 2: Identifying the Child Node in the Doubling Relationship
Complete Statement:
...must be exactly double the value assigned to the principal node labeled [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: the principal node labeled [BLANK 2]
Meaning: This refers to the node whose value is half of the previously identified parent node.
Relation to Chart: Look for the node that the parent points to with the arrow.
- Key Phrase: the principal node labeled [BLANK 2]
- Statement Breakdown 2:
- Key Phrase: exactly double
Meaning: The parent node's value is twice this node's value.
Relation to Chart: Direction of the arrow confirms which node is the child.
- Key Phrase: exactly double
- What is needed: Which principal node is the recipient (child) in the doubling relationship identified above?
Solution:
- Condensed Solution Implementation:
Refer to the diagram and see which node receives the arrow from the parent. Since D points to A, A is half the value of D. - Necessary Data points:
The arrow direction from D (parent) to A (child) means A's value is half of D's.
Calculations Estimations:
No calculation needed; direct observation shows A as the child node.
Comparison to Answer Choices:
A is the only node directly linked by D's arrow indicating the doubling relationship.
FINAL ANSWER Blank 2: A
Summary
By carefully examining the network diagram, we see that node D has a direct connection (arrow) to node A, showing D's value is double A's (\(\mathrm{D = 2 \times A}\)). Thus, D fills the first blank as the parent node and A fills the second blank as the child node in this doubling relationship.
Question Independence Analysis
These two blanks are dependent: identifying the parent node (Blank 1) directly determines the child node (Blank 2) in the network's doubling relationship.