In Nation X, all citizens aged 18 or older are eligible to vote and all citizens under age 18 are...
GMAT Graphics Interpretation : (GI) Questions
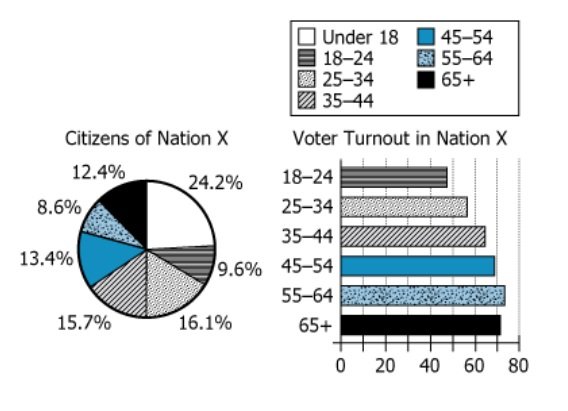
In Nation X, all citizens aged 18 or older are eligible to vote and all citizens under age 18 are not. The left graph shows the percentage of citizens of Nation X who fell within various age ranges at the time of the last election. For the same age ranges during that election, the right graph shows the voter turnout—the percentage of eligible voters who voted.
Select from each drop-down menu the option that creates the most accurate statement based on the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Voting eligibility rule | "all citizens aged 18 or older are eligible to vote and all citizens under age 18 are not" | Citizens 18+ can vote, under 18s cannot |
| Left graph description | "shows the percentage of citizens of Nation X who fell within various age ranges at the time of the last election" | Pie chart shows age-group shares of whole population |
| Right graph description | "shows the voter turnout—the percentage of eligible voters who voted" | Bar chart shows what % of eligible voters actually voted, by age group |
Table 2: Chart Analysis
| Chart Component | What's Shown | What This Tells Us |
|---|---|---|
| Chart types | Pie chart (left) and bar chart (right) | Two complementary displays: demographics and turnout rates |
| Pie chart data | Age groups (with %): Under 18 (24.2%), 18-24 (9.6%), 25-34 (16.1%), 35-44 (15.7%), 45-54 (13.4%), 55-64 (8.6%), 65+ (12.4%) | 24.2% are under 18 and not eligible; other groups make up the eligible voters |
| Bar chart data | Turnout rates: 18-24 (47%), 25-34 (56%), 35-44 (64%), 45-54 (69%), 55-64 (73%), 65+ (71%) | Turnout rises with age—older people vote more; 55-64 group votes the most |
| Visual pattern | Pie: under 18 largest group; Bar: steady increase in turnout by age until 65+ | Youth underrepresented among voters; elderly most likely to vote |
Key Insights
- Only citizens 18+ (totaling \(75.8\%\) of population) are eligible voters—this filters the dataset for turnout and probability questions.
- Voter turnout is strongly age-dependent, rising steadily from 18-24 (47%) to 55-64 (73%), with a slight dip at 65+ (71%).
- To compute the chance a random eligible voter is from a given age group, divide that group's % (from the pie chart) by \(75.8\%\).
- To find the chance a random eligible voter both voted and is from a given age group, multiply that group's population % by its turnout rate, then divide by \(75.8\%\).
- The dataset enables comparison of population structure and participation, revealing both demographic bottlenecks and behavioral patterns.
Step-by-Step Solution
Question 1: Probability of Random Eligible Voter Being Age 25-34
Complete Statement:
If a citizen of Nation X who was eligible to vote at the time of the last election was selected at random, the probability that the citizen was age 25 to 34 is, to the nearest percent, [BLANK 1]
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: citizen of Nation X who was eligible to vote
- Meaning: This means we're only looking at people old enough to vote (i.e., age 18 and over).
- Relation to Chart: The chart shows that 24.2% of citizens are under 18 and thus not eligible; the remaining \(75.8\%\) are eligible voters.
- Important Implications: Probabilities should be found out of the eligible group, not the total population.
- Statement Breakdown 2:
- Key Phrase: probability that the citizen was age 25 to 34
- Meaning: What percentage of eligible voters are in the 25-34 age group.
- Relation to Chart: The chart shows 16.1% of all citizens are age 25-34.
- Important Implications: We must adjust this percentage to reflect only eligible voters (by dividing 16.1% by \(75.8\%\)).
- What is needed: The percentage of eligible voters who are 25-34 years old.
Solution:
- Condensed Solution Implementation:
Divide the percentage of all citizens who are 25-34 by the percentage of the population that is eligible to vote. - Necessary Data points:
Population under 18: 24.2%. Population 25-34: 16.1%. Eligible voter proportion: \(75.8\%\).- Calculations Estimations:
\(\frac{16.1\%}{75.8\%} = 0.212 = 21\%\) - Comparison to Answer Choices:
Answer choices: 12%, 16%, 21%, 56%. 21% matches the calculation and is the correct answer.
- Calculations Estimations:
FINAL ANSWER Blank 1: 21%
Question 2: Probability of Random Eligible Voter Who Both Voted and Was Age 25-34
Complete Statement:
and the probability that the citizen both voted in the last election and was age 25 to 34 is, to the nearest percent, [BLANK 2]
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: both voted in the last election and was age 25 to 34
- Meaning: We are finding what percent of eligible voters are 25-34 AND actually voted in the last election.
- Relation to Chart: Need both the population proportion (16.1% are 25-34) and the turnout for this age group (56%).
- Statement Breakdown 2:
- Key Phrase: probability
- Meaning: What percent of eligible voters meet BOTH criteria.
- Relation to Chart: Multiply the proportion in the age group by the turnout, then adjust by eligible population.
- What is needed: The percentage of eligible voters who both voted and were age 25-34.
Solution:
- Condensed Solution Implementation:
First, multiply the percent of all citizens who are 25-34 by the turnout for that group. Then, divide by the percentage of the population eligible to vote. - Necessary Data points:
25-34 age group: 16.1% of citizens. Turnout for 25-34: 56%. Eligible voters: \(75.8\%\) of citizens.- Calculations Estimations:
\(16.1\% \times 56\% = 9.016\%\)
\(\frac{9.016\%}{75.8\%} = 0.119 = 12\%\) - Comparison to Answer Choices:
Answer choices: 10, 12, 21, 56. 12 matches the calculation and is the correct answer.
- Calculations Estimations:
FINAL ANSWER Blank 2: 12
Summary
For Blank 1, we found that 21% of eligible voters were age 25-34 by dividing the percentage of all citizens in that age range by the percentage eligible to vote. For Blank 2, we calculated the percent of eligible voters who both voted and were age 25-34 by multiplying the age group's population percentage by its turnout, then dividing by eligible population, resulting in approximately 12%.
Question Independence Analysis
The two blanks are related because the calculation for Blank 2 uses the result from Blank 1 and applies the turnout percentage, so the answer to Blank 2 depends directly on how Blank 1 is calculated.