In Country X, a building is in Category A if it has a roof height of at least 350 meters....
GMAT Graphics Interpretation : (GI) Questions
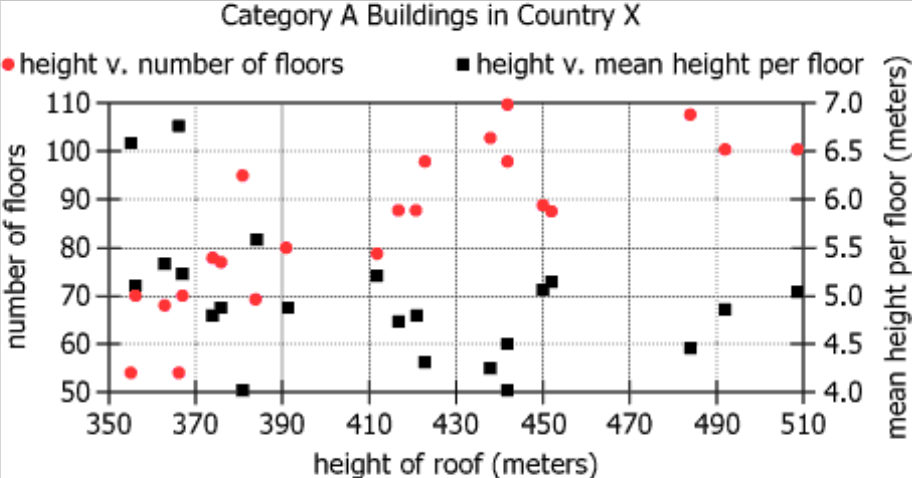
In Country X, a building is in Category A if it has a roof height of at least 350 meters. In the graph, each of the 22 Category A buildings is represented by two points arranged vertically: one representing the comparison of the height of the building's roof to the number of floors (red circles), the other representing the comparison of the height of the building's roof to the mean height per floor (black squares).
Based on the given information, use the drop-down menus to most accurately complete the following statements about Category A buildings in Country X.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Content | Interpretation |
|---|---|---|
| Category A definition | A building is in Category A if it has a roof height of at least 350 meters | Category A buildings: roof height \(\geq 350 \text{ m}\) |
| Number of buildings | 22 Category A buildings | Dataset consists of 22 buildings |
| Data representation | Each building represented by two vertically arranged points | Each building shown twice in the chart |
| Red circle meaning | Height vs number of floors (red circles) | Red = relationship: roof height & floor count |
| Black square meaning | Height vs mean height per floor (black squares) | Black = relationship: height & avg floor ht |
Table 2: Chart Analysis
| Chart Element | Description | Observation/Insight |
|---|---|---|
| Chart Type | Scatter plot, dual data series | Red circles & black squares vertically pair per building |
| X-axis | Roof height (\(350\text{–}510 \text{ meters}\)) | Tallest buildings shown; Category A threshold identified |
| Left Y-axis | Number of floors (\(50\text{–}110\)) | Buildings range from 50 to 110 floors |
| Right Y-axis | Mean height per floor (\(4.0\text{–}7.0 \text{ meters}\)) | Floor heights range from 4.0 to 7.0 meters |
| Red circle trend | Correlates roof height and number of floors | Taller buildings generally have more floors |
| Black square trend | Correlates roof height and mean height per floor | Taller buildings generally have lower mean floor heights |
| Outlier/highest value | Highest black square at lowest (\(350\text{–}370 \text{ m}\)) roof height | Greatest mean height per floor is for shorter Category A bldg |
Key Insights
- The building with the greatest mean height per floor (\(\sim 6.8 \text{ m}\)) has a roof height between \(350\text{–}370 \text{ meters}\).
- There is a negative correlation between the number of floors and the mean height per floor in Category A buildings: more floors, lower average floor height.
- Taller Category A buildings tend to achieve height by increasing floor count while the average floor height decreases.
Step-by-Step Solution
Question 1: Finding the Roof Height Range for the Building with the Greatest Mean Height per Floor
Complete Statement:
The building with the greatest mean height per floor has a roof height between [BLANK] meters.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: greatest mean height per floor
- Meaning: We're searching for the building that has the highest average height for each floor.
- Relation to Chart: This value is represented by the highest black square on the chart (mean height per floor on the right y-axis).
- Important Implications: The building with the greatest mean height per floor may not be the tallest overall building.
- Statement Breakdown 2:
- Key Phrase: roof height between [BLANK] meters
- Meaning: We need the x-axis range (roof height) in which this building falls.
- Relation to Chart: Find the highest black square's horizontal location to match with the given x-axis ranges.
- Important Implications: The answer must be chosen from one of the given ranges, like \(350\text{–}370 \text{ meters}\).
- What is needed: The range of roof height (on the x-axis) where the highest black square (mean height per floor) is located.
Solution:
- Condensed Solution Implementation:
Locate the highest black square on the graph and match its x-axis position to the set of provided ranges. - Necessary Data points:
Visual position of black squares on the chart, especially the one at the highest mean height per floor (y-axis right side). - Calculations Estimations:
No calculation needed; just visual identification. The black square at the far left (the \(350\text{–}370 \text{ meters}\) range) is the highest. - Comparison to Answer Choices:
Compared with the options, the correct roof height range is \(350\text{–}370 \text{ meters}\).
FINAL ANSWER Blank 1: 350 and 370
Question 2: Determining the Correlation Between Number of Floors and Mean Height per Floor
Complete Statement:
There is a [BLANK] correlation between the number of floors and the mean height per floor.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: correlation between the number of floors and the mean height per floor
- Meaning: We must decide what kind of relationship (if any) the two variables have.
- Relation to Chart: Red circles (number of floors, left y-axis) versus black squares (mean height per floor, right y-axis) as roof height increases.
- Statement Breakdown 2:
- Key Phrase: [BLANK] correlation
- Meaning: The type of connection: positive, negative, or negligible.
- Relation to Chart: Watch if high points on one measure are associated with high or low points on the other.
- What is needed: Whether the correlation is strong positive, negligible, or strong negative.
Solution:
- Condensed Solution Implementation:
Observe the overall trends: do buildings with more floors tend to have higher or lower mean floor heights? - Necessary Data points:
As roof height increases, red circles show more floors; black squares (mean height per floor) drop lower. - Calculations Estimations:
As one measure rises, the other falls: this is a strong negative correlation. - Comparison to Answer Choices:
The downward trend in one variable as the other increases matches 'Strong Negative' correlation.
FINAL ANSWER Blank 2: Strong Negative
Summary
For question 1, visually identify which building (black square) is highest on the mean height per floor axis, which falls in the \(350\text{–}370 \text{ m}\) roof height range. For question 2, the chart demonstrates a strong negative correlation between number of floors and mean height per floor: as one increases, the other decreases.
Question Independence Analysis
The questions are independent. Question 1 asks for the location of a specific data point, while Question 2 asks about the overall relationship between two variables; answering one doesn't affect answering the other.