In Country X, a ballroom is classified as Category C if it has a ceiling of at least 10 meters....
GMAT Graphics Interpretation : (GI) Questions
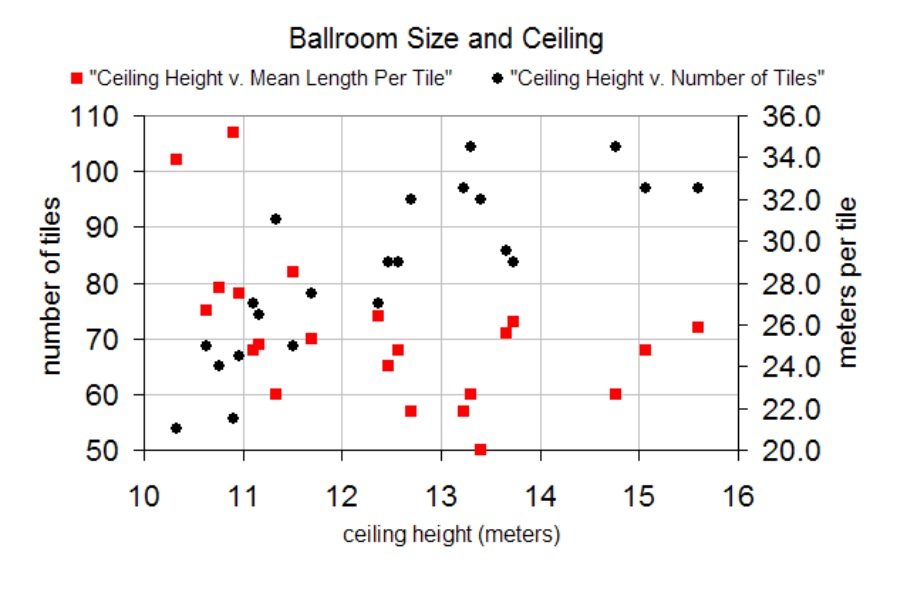
In Country X, a ballroom is classified as Category C if it has a ceiling of at least 10 meters. In the graph, each of the 22 Category C ballrooms is represented by two points arranged vertically: one representing the comparison of the height of the ballroom's ceiling to the number of tiles in the ballroom area (black circles), the other representing the comparison of the height of the ballroom's ceiling to the mean length per tile in the ballroom area (red squares).
Based on the given information, use the drop-down menus to most accurately complete the following statements about Category C ballrooms in Country X.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Geographic Context | In Country X | The data refers to ballrooms within Country X |
| Category C Definition | A ballroom is classified as Category C if it has a ceiling of at least 10 meters | If a ballroom has a ceiling 10 meters or higher, it's considered Category C |
| Data Sample Size | Each of the 22 Category C ballrooms | Data is provided for all 22 Category C ballrooms in Country X |
| Data Representation | Each ballroom is represented by two points arranged vertically | Every ballroom appears as two vertically aligned points on the graph |
| Black Circles Meaning | Comparison of ceiling height to number of tiles (black circles) | Black circles plot ceiling height vs. how many tiles each ballroom has |
| Red Squares Meaning | Comparison of ceiling height to mean length per tile (red squares) | Red squares plot ceiling height vs. average tile size in each ballroom |
Table 2: Chart Analysis
| Chart Component | What's Shown | Interpretation |
|---|---|---|
| X-axis | Ceiling height (meters), range: 10–16 | All ballrooms charted have ceilings between 10 and 16 meters, reflecting Category C |
| Left Y-axis | Number of tiles, range: 50–110 | Ballrooms have between 50 and 110 tiles each |
| Right Y-axis | Mean length per tile (meters), range: 20–36 | Tile sizes (mean per ballroom) range from 20 to 36 meters |
| Data Points | Vertical pairs: black circle (tiles), red square (tile size) for each ballroom | Each ballroom's tile count and average tile size are plotted at the same ceiling height |
| Highest Mean Tile Size | Red square peaks near ceiling height 11 meters | Ballroom with the largest average tile has 11m ceiling |
| Black and Red Relationship | Black and red points are inversely related | More tiles means smaller average tile size, and vice versa |
Key Insights
- The ballroom with the largest mean tile size (~36 meters per tile) has a ceiling height of about 11 meters.
- Ballrooms with more tiles tend to have a smaller average tile size, indicating an inverse relationship between tile count and tile size.
- All Category C ballrooms have ceiling heights between 10 and 16 meters, directly matching the 'at least 10m' definition.
- The inverse relationship observed is logical: for a given floor area, increasing the number of tiles decreases the average size of each tile.
Step-by-Step Solution
Question 1: Ceiling Height of Ballroom with Greatest Mean Tile Length
Complete Statement:
The ballroom with the greatest mean length per ballroom tile has a ceiling height _____ meters.
Breaking Down the Statement
• Statement Breakdown 1:
- Key Phrase: The ballroom with the greatest mean length per ballroom tile
_ Meaning: Identify which ballroom has the largest average length per tile.
_ Relation to Chart: Look for the highest red square on the graph, as red squares represent mean length per tile.
_ Important Implications: This is asking for a specific data point: which x-value (ceiling height) has the highest red square (mean length per tile).
• Statement Breakdown 2:
- Key Phrase: has a ceiling height _____ meters
_ Meaning: Find the ceiling height associated with that maximum mean length per tile.
_ Relation to Chart: Check the x-axis value directly below the highest red square.
_ Important Implications: Choose the answer that covers the estimated ceiling height based on the graph's scale and answer choices.
• What is needed: The ceiling height (in meters) where the mean length per tile is the highest among all ballrooms.
Solution:
- Condensed Solution Implementation:
Scan the plot for the red square that is the highest on the right y-axis, then note its ceiling height from the x-axis. - Necessary Data points:
The highest red square on the right y-axis (mean tile length, in meters per tile); the corresponding ceiling height from the x-axis.
_ Calculations Estimations:
The highest red square peaks around 36 meters on the right y-axis at a ceiling height of approximately 11 meters.
_ Comparison to Answer Choices:
11 meters fits the option 'Between 10-12' meters; other ranges (12-14, 14-16, 16+) do not fit.
FINAL ANSWER Blank 1: Between 10-12
Question 2: Correlation Between Number of Tiles and Mean Tile Length
Complete Statement:
There is a _____ correlation between the number of ballroom tiles and the mean length per ballroom tile.
Breaking Down the Statement
• Statement Breakdown 1:
- Key Phrase: correlation between the number of ballroom tiles and the mean length per ballroom tile
_ Meaning: Determine the direction and strength of association between the two variables across the dataset.
_ Relation to Chart: Compare patterns between the heights of black circles (number of tiles) and red squares (mean length per tile) at each ceiling height.
• Statement Breakdown 2:
- Key Phrase: There is a _____ correlation
_ Meaning: Classification of the relationship as Strong Positive, Negligible, or Strong Negative.
_ Relation to Chart: Analyze whether increases in the number of tiles correspond to increases, decreases, or no pattern in mean tile length.
• What is needed: The strength and direction of the relationship between number of tiles (black circles) and mean tile length (red squares) across all ballrooms: strong negative, strong positive, or negligible.
Solution:
- Condensed Solution Implementation:
Examine whether high numbers of tiles occur alongside high or low mean lengths per tile across the chart. - Necessary Data points:
Visual comparison of black circles (left y-axis, number of tiles) and red squares (right y-axis, mean length per tile) at every ceiling height.
_ Calculations Estimations:
As the number of tiles increases (black circles higher), the mean length per tile decreases (red squares lower), showing a consistent inverse relationship.
_ Comparison to Answer Choices:
A strong negative relationship is clear because, overall, the data points move in opposite directions, fitting the 'Strong Negative' option.
FINAL ANSWER Blank 2: Strong Negative
Summary
By visually analyzing the graph, the ballroom with the highest mean tile length is at a ceiling height of about 11 meters, corresponding to the answer 'Between 10-12'. When examining the number of tiles and the mean length per tile for all ballrooms, there's a consistent inverse pattern: more tiles are associated with shorter average lengths per tile, clearly indicating a 'Strong Negative' correlation.
Question Independence Analysis
The two blanks are independent. The first asks for a specific data point (the ceiling height of the ballroom with the highest mean tile length), and the second asks for a general relationship pattern (the correlation between two variables). There is no logical or mathematical dependence between the answers to these two questions.