In Country C, the numbers of transactions made by various noncash methods in 2006 and 2009 are shown in the...
GMAT Graphics Interpretation : (GI) Questions
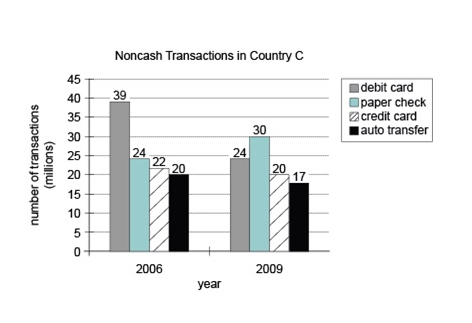
In Country C, the numbers of transactions made by various noncash methods in 2006 and 2009 are shown in the graphic. All other transactions were made with cash.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Geographic context | In Country C | Data is for Country C only |
| Data type | numbers of transactions | Chart counts transactions, not amounts or percentages |
| Payment methods | various noncash methods | Multiple ways to pay without cash are charted |
| Time periods | in 2006 and 2009 | Compares two distinct years (2006 and 2009) |
| Cash context | All other transactions were made with cash | Cash is used but not shown in the chart |
Table 2: Chart Analysis
| Chart Component | What's Shown | What This Tells Us |
|---|---|---|
| Chart type | Grouped bar chart (by year and method) | Enables direct comparison of noncash payment methods by year |
| Y-axis | Number of transactions (millions), 0–45 scale | All bar heights are in millions; e.g., 39 means 39 million |
| Payment methods | Debit card, paper check, credit card, auto transfer | These are all the noncash methods measured in Country C |
| Data labels | Exact values on bars | Transaction counts can be read precisely, without estimation |
| Visual pattern | Most methods decline; paper check rises | Paper check is notable as the only method that increased |
Key Insights
Paper check is the only noncash method that increased in use (from 24 to 30 million: a 25% rise), while debit cards showed the steepest decline (from 39 to 24 million). Total noncash transactions dropped from 105 million in 2006 to 91 million in 2009, marking an overall decrease in noncash use. Credit card transactions fell slightly (22 to 20 million), but were notable for a 10% rise in total value, indicating a higher average transaction amount.
Step-by-Step Solution
Question 1: Change in Average Credit Card Transaction Value
Complete Statement:
If the total value of all credit card transactions in 2009 was 10% more than the total value of all credit card transactions in 2006, then the average (arithmetic mean) value of credit card transactions increased by ___% from 2006 to 2009.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: total value of all credit card transactions in 2009 was 10% more than the total value of all credit card transactions in 2006
- Meaning: The sum of money from all credit card transactions went up by 10% from 2006 to 2009.
- Relation to Chart: While the chart shows the number of transactions, it does not display the total monetary value. This information is given in the question.
- Important Implications: We must factor this 10% increase in total value into any calculation concerning the average transaction value.
Statement Breakdown 2:
- Key Phrase: average (arithmetic mean) value of credit card transactions
- Meaning: This is found by dividing the total value by the number of transactions.
- Relation to Chart: The number of credit card transactions is shown in the chart: 22 million in 2006 and 20 million in 2009.
- Important Implications: To find the average for each year, we divide total value by number of transactions, then compare the two years.
What is needed: The percent increase in the average credit card transaction value from 2006 to 2009.
Solution:
- Condensed Solution Implementation:
Use the given percent increase in total value and the percent decrease in number of transactions to calculate the change in the average value. Average = Total Value / Number of Transactions. - Necessary Data points:
Credit card transactions: 22 million in 2006, 20 million in 2009. Total value: increase by 10%.- Calculations Estimations:
The total value increases by a factor of 1.10, while the number of transactions decreases by \\(\frac{2}{22} \approx 0.09\\) (about 9%) to 0.91 of the original. So, new average = \\(\frac{1.10}{0.91} \approx 1.21\\). Percent increase = (1.21 - 1) × 100% = 21%. - Comparison to Answer Choices:
The answer choices include 21.0%, so 21.0 is correct.
- Calculations Estimations:
FINAL ANSWER Blank 1: 21.0
Question 2: Transaction Type with 25% Increase
Complete Statement:
The number of ___ transactions increased by 25% from 2006 to 2009.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: number of ___ transactions
- Meaning: We're looking for which payment method had its number of transactions increase.
- Relation to Chart: The chart directly shows transaction counts for 2006 and 2009 for each method.
Statement Breakdown 2:
- Key Phrase: increased by 25%
- Meaning: The 2009 value should be 1.25 times the 2006 value.
- Relation to Chart: Calculation must be done for each method: (2009 - 2006)/2006 × 100%.
What is needed: Which payment method increased by exactly 25% in number of transactions from 2006 to 2009.
Solution:
- Condensed Solution Implementation:
Find the numerical increase for each method and compare to its 2006 value. Look for a 25% increase. - Necessary Data points:
Debit card: 39 → 24 million (decrease), Paper check: 24 → 30 million (increase), Credit card: 22 → 20 million (decrease), Auto transfer: 20 → 17 million (decrease).- Calculations Estimations:
Paper check increased by 6 million, from 24 to 30. Fractional change: \\(\frac{6}{24} = 0.25 = 25\%\\). - Comparison to Answer Choices:
Only Paper Check shows an increase, and the increase is exactly 25%, fitting the blank.
- Calculations Estimations:
FINAL ANSWER Blank 2: Paper Check
Summary
The first blank required combining a 10% increase in total value with a 9% decrease in number to get a 21% increase in average value. The second blank needed identifying that Paper Check transactions rose by exactly 25%. Both could be solved directly from the chart and given info.
Question Independence Analysis
The two blanks are independent. The first is about percent change in average value for credit cards, the second about identifying which payment method increased by 25% in raw count. Solving one does not give or require information for solving the other.