In a certain geographic area, bus companies set their ticket prices based on the number of kilometers that a passenger...
GMAT Graphics Interpretation : (GI) Questions
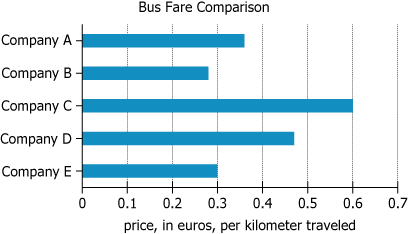
In a certain geographic area, bus companies set their ticket prices based on the number of kilometers that a passenger travels on a given trip. For each of 5 different bus companies operating in that area, the chart gives the price that they charge, in euros, per kilometer traveled.
Select from each drop-down menu the option that creates the most accurate statement based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Geographic Context | In a certain geographic area | The dataset refers to a specific but unnamed region |
| Pricing Model | Bus companies set their ticket prices based on the number of kilometers... | Fares depend on trip distance |
| Number of Companies | 5 different bus companies | Information is about exactly 5 companies |
| Chart Description | The chart gives the price they charge, in euros, per kilometer traveled | The chart shows each company's per-kilometer price in euros |
Table 2: Chart Analysis
| Chart Component | What Is Shown | Interpretation / Key Data |
|---|---|---|
| Chart Type | Horizontal bar chart; 5 companies (A-E) | Visualizes per-kilometer pricing of each company |
| X-axis | Euros per kilometer, 0 to 0.7 | Scale captures full price spread; maximum is just over 0.6 |
| Y-axis | Company names labeled A, B, C, D, E | Companies are listed alphabetically, not by fare ranking |
| Highest Bar | Company C: \(0.6\) euros per kilometer | Company C charges the highest rate |
| Lowest Bar | Company B: approx. \(0.28\) euros per kilometer | Company B charges the lowest rate |
| Exact Ratio | Company C: \(0.6\), Company E: \(0.3\) | Company C charges exactly double Company E's rate |
Key Insights
Company C charges exactly twice as much as Company E (\(0.6\) vs \(0.3\) euros per kilometer). Company C is a strong outlier with the highest fare, while Company B has the lowest. The per-kilometer prices among the five companies range from approximately \(0.28\) to \(0.6\) euros, showing substantial variation. The chart arranges companies alphabetically, so price relationships require visual attention.
Step-by-Step Solution
Question 1: Identifying the Company That Charges Twice as Much
Complete Statement:
Company [BLANK 1] charges twice as much per kilometer traveled as does Company [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: charges twice as much per kilometer
- Meaning: The fare of one company must be exactly double that of another company.
- Relation to Chart: Look for two companies where one's bar is precisely two times the other in height (value).
- Important Implications: We're searching for an exact \(2:1\) ratio between two companies' prices, not an estimate.
- Key Phrase: charges twice as much per kilometer
- Statement Breakdown 2:
- Key Phrase: Company [BLANK 1]
- Meaning: The company with the higher price per kilometer within the \(2:1\) pair.
- Relation to Chart: This will be the taller (higher value) bar of the two that form the \(2:1\) ratio.
- Important Implications: Once this company is found, the company it is twice as expensive as can also be identified.
- Key Phrase: Company [BLANK 1]
- What is needed: The company whose fare is exactly twice that of another company.
Solution:
- Condensed Solution Implementation:
Scan the chart for pairs of companies and calculate if any have an exact \(2:1\) ratio in fares. This can be done by dividing the fare of each company by the fares of all other companies. - Necessary Data points:
Company fares: A (\(0.35\) Euro/km), B (\(0.28\) Euro/km), C (\(0.60\) Euro/km), D (\(0.47\) Euro/km), E (\(0.30\) Euro/km).- Calculations Estimations:
C \((0.60) / E (0.30) = 2\), which is an exact \(2:1\) ratio. - Comparison to Answer Choices:
Only Company C's fare is exactly twice that of another company (E). Therefore, the answer for [BLANK 1] is C.
- Calculations Estimations:
FINAL ANSWER Blank 1: C
Question 2: Identifying the Company That Is Half as Expensive
Complete Statement:
Company C charges twice as much per kilometer traveled as does Company [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: Company C charges twice as much
- Meaning: Company C has a fare exactly two times higher than the company in [BLANK 2].
- Relation to Chart: Find the company whose fare, when doubled, equals Company C's fare.
- Key Phrase: Company C charges twice as much
- Statement Breakdown 2:
- Key Phrase: as does Company [BLANK 2]
- Meaning: The company with half the fare rate of Company C.
- Relation to Chart: This will be the shortest bar with a value such that \(2 \times\) its value = Company C's value.
- Key Phrase: as does Company [BLANK 2]
- What is needed: Which company charges half the fare of Company C.
Solution:
- Condensed Solution Implementation:
Divide Company C's fare by 2 and see which company has that fare. - Necessary Data points:
Company C: \(0.60\) Euro/km. \(0.60 / 2 = 0.30\) Euro/km.- Calculations Estimations:
Company E charges \(0.30\) Euro/km, which matches the calculation. - Comparison to Answer Choices:
Company E is the only company whose fare is half of Company C's fare. So, [BLANK 2] is E.
- Calculations Estimations:
FINAL ANSWER Blank 2: E
Summary
By inspecting the fares, we find that Company C (\(0.60\) Euro/km) is exactly twice as expensive as Company E (\(0.30\) Euro/km). No other company pair fits this exact \(2:1\) relationship.
Question Independence Analysis
The blanks are not independent: once we identify that C charges exactly twice as much as E, both answers are determined by this unique \(2:1\) relationship.