In a certain game, each player's turn consists of drawing a card from a randomized deck and immediately carrying out...
GMAT Graphics Interpretation : (GI) Questions
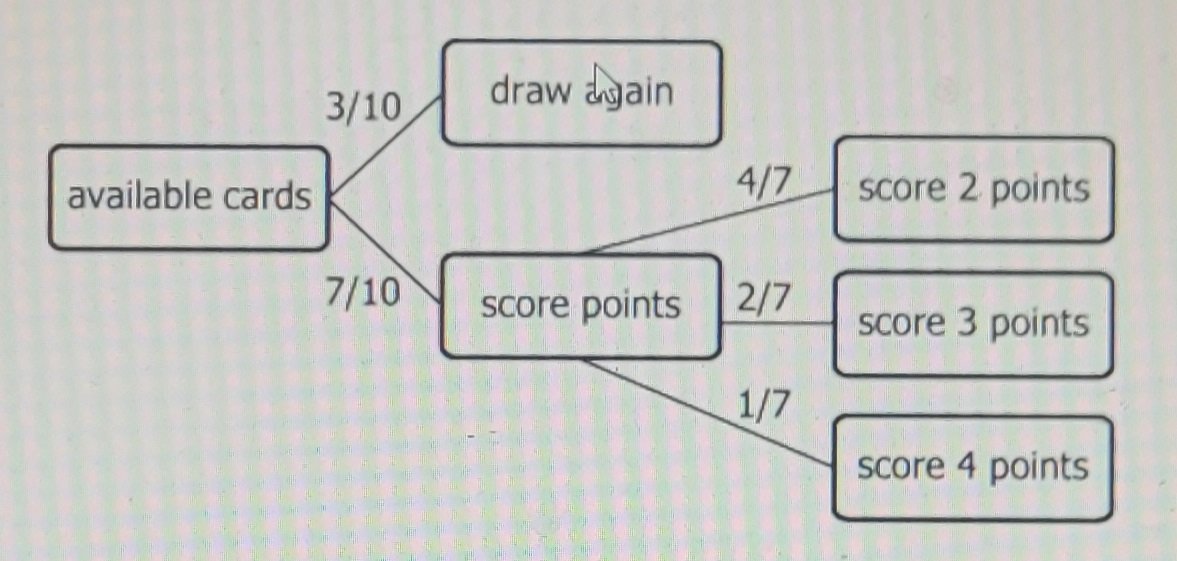
In a certain game, each player's turn consists of drawing a card from a randomized deck and immediately carrying out the instructions on the card. For example, if the card's instruction is to draw again, the player immediately draws another card and carries out that card's instruction. After the instruction is carried out, the card is removed from the game, and, except when the card instruction is to draw again, the player's turn ends. It is currently Mardea's turn, and she knows that each of the remaining cards instructs the player to do exactly one of the following: score 2 points, score 3 points, score 4 points, or draw again. Mardea will win the game this turn if and only if she scores 3 or more points on this turn. The diagram shows the probabilities associated with the possible outcomes for the next card that is drawn.
Select from the drop-down menus the options that complete the statement so that it is accurate based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Game mechanics | each player's turn consists of drawing a card from a randomized deck and immediately carrying out the instructions on the card | Players draw a card and immediately follow its instruction |
| Card removal rule | After the instruction is carried out, the card is removed from the game | Used cards are not returned to the deck |
| Turn end condition | except when the card instruction is to draw again, the player's turn ends | The only way to keep taking actions is to get a 'draw again' card; otherwise, your turn ends after one card |
| Current player | It is currently Mardea's turn | Mardea is the active player for this probability question |
| Remaining card types | each of the remaining cards instructs the player to do exactly one of the following: score 2 points, score 3 points, score 4 points, or draw again | Exactly four possible card instructions remain in the deck |
| Win condition | Mardea will win the game this turn if and only if she scores 3 or more points on this turn | Mardea must score at least 3 points in her turn to win |
| Probability diagram | The diagram shows the probabilities associated with the possible outcomes for the next card that is drawn | There is a visual representation of drawing each type of card and associated probabilities |
Table 2: Chart Analysis
| Chart Component | What's Shown | Key Notes |
|---|---|---|
| Tree diagram root | available cards | Represents the set of all possible remaining cards |
| First branching | \(\frac{3}{10}\) to 'draw again', \(\frac{7}{10}\) to 'score points' | 30% chance of 'draw again', 70% for scoring |
| Score points branch | splits: \(\frac{4}{7}\) to 'score 2', \(\frac{2}{7}\) to 'score 3', \(\frac{1}{7}\) to 'score 4' | If 'score points', probability is distributed among the three point-value cards |
| Outcome probabilities | \(\frac{3}{10}\) draw again, \(\frac{4}{10}\) score 2, \(\frac{2}{10}\) score 3, \(\frac{1}{10}\) score 4 | Probabilities for all immediate outcomes sum to 1 |
| Path structure | 'Draw again' leads to further draws. 'Score X' ends turn | The only way to have multiple draws is to get 'draw again' card |
Key Insights
The only way Mardea draws more than one card in a turn is if her first card instructs her to 'draw again', which has a probability of \(\frac{3}{10}\). All other initial outcomes end her turn after one card. Scoring 3 or more points in a turn is only directly possible by drawing 'score 3' or 'score 4' as the first card, or by drawing combinations after a 'draw again'. The probability tree structure highlights all possible draw outcomes and their likelihoods, emphasizing the special role of the 'draw again' card.
Step-by-Step Solution
Question 1: Numerator of Probability Fraction
Complete Statement:
The probability that Mardea will draw at least 2 cards this turn is [BLANK 1] in...
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: draw at least 2 cards this turn
Meaning: Mardea has to pick 2 or more cards during her current turn.
Relation to Chart: The chart (tree diagram) outlines what happens after each card drawn and the chance of each event.
Important Implications: We need to pinpoint when a turn continues, allowing further card draws (specifically: only if the card is 'draw again').
- Key Phrase: draw at least 2 cards this turn
- Statement Breakdown 2:
- Key Phrase: probability that Mardea will...
Meaning: We are looking for the likelihood of a certain event based on the provided probabilities.
Relation to Chart: Probabilities of each possible outcome for the first card are shown directly on the chart.
Important Implications: We use the chart to find which outcome(s) permit additional cards to be drawn.
- Key Phrase: probability that Mardea will...
- What is needed: The numerator (top value) of the probability fraction for Mardea drawing at least 2 cards in her turn.
Solution:
- Condensed Solution Implementation:
A player draws 2 or more cards if (and only if) their first card says 'draw again.' Otherwise, the turn ends. The probability of drawing a 'draw again' card first is shown as \(\frac{3}{10}\). - Necessary Data points:
Probability of first card being 'draw again' = \(\frac{3}{10}\) (from the tree diagram).- Calculations Estimations:
So, the probability of at least 2 cards is simply \(\frac{3}{10}\). - Comparison to Answer Choices:
Numerator is 3, as \(\frac{3}{10}\) matches an option. '3' is listed among the provided choices.
- Calculations Estimations:
FINAL ANSWER Blank 1: 3
Question 2: Denominator of Probability Fraction
Complete Statement:
The probability that Mardea will draw at least 2 cards this turn is 3 in [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: 3 in [BLANK 2]
Meaning: Probability is being expressed as a fraction 3/[BLANK 2].
Relation to Chart: The denominator should complete the fraction with the correct total outcomes (from the chart's probability denominator).
- Key Phrase: 3 in [BLANK 2]
- What is needed: The denominator (bottom value) of the probability fraction for this event.
Solution:
- Condensed Solution Implementation:
The probability is \(\frac{3}{10}\) according to the tree diagram probabilities. - Necessary Data points:
Denominator from the fraction expressing total possible first-card outcomes is 10.- Calculations Estimations:
The fraction \(\frac{3}{10}\) indicates the denominator is 10. - Comparison to Answer Choices:
Among the given options ([8, 9, 10]), the correct denominator is 10.
- Calculations Estimations:
FINAL ANSWER Blank 2: 10
Summary
In this scenario, Mardea can only draw multiple cards if her first card says 'draw again', which has a probability of \(\frac{3}{10}\) based on the tree diagram. Expressing this as '3 in 10' directly answers both blanks.
Question Independence Analysis
The blanks are dependent, as they combine to form the fraction representing the total probability (numerator/denominator) for the event in question.