For each of the 11 employees of a small company, the graphic shows the employee's salary (as a percent of...
GMAT Graphics Interpretation : (GI) Questions
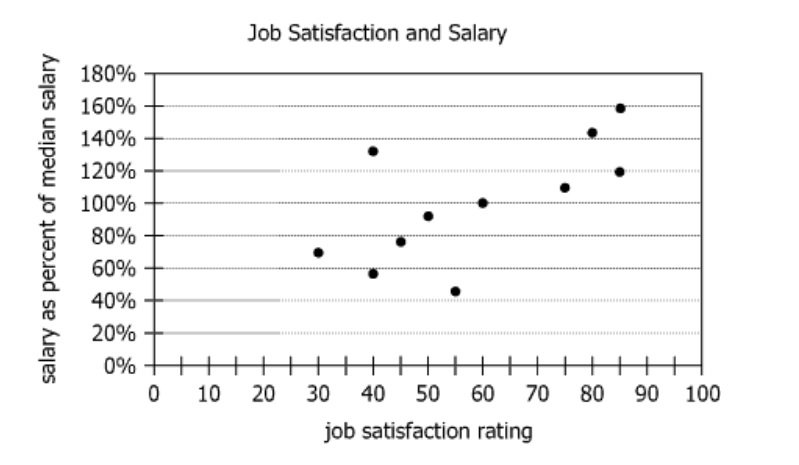
For each of the 11 employees of a small company, the graphic shows the employee's salary (as a percent of the company's median salary) and job satisfaction rating (given as a number between 0 and 100, where a higher rating represents greater job satisfaction).
From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Company size | For each of the 11 employees of a small company | The dataset includes all 11 employees in a small company |
| Salary measurement | the employee's salary (as a percent of the company's median salary) | Each employee's salary is shown as a percent relative to the median |
| Job satisfaction scale | job satisfaction rating (given as a number between 0 and 100, where a higher rating represents greater job satisfaction) | Satisfaction is measured from \(\mathrm{0}\) (lowest) to \(\mathrm{100}\) (highest) |
Table 2: Chart Analysis
| Chart Component | Description/Values | Key Takeaway |
|---|---|---|
| Chart type | Scatter plot with one point per employee | Compares salary (y) and satisfaction (x) for each employee |
| X-axis | Job satisfaction: \(\mathrm{0}\) to \(\mathrm{100}\) | Higher values mean higher satisfaction |
| Y-axis | Salary as % of company median: approx \(\mathrm{40\%}\) to \(\mathrm{180\%}\) | \(\mathrm{100\%}\) = median salary value |
| Data distribution | Most points slope upward; one point at lowest salary | General trend: higher salary ↔ higher satisfaction |
| Key outlier | \(\mathrm{(55, 46)}\): Median satisfaction, but lowest salary | Median satisfaction owned by person with lowest salary |
Key Insights
The employee with the median job satisfaction rating (\(\mathrm{55}\)) earns the lowest salary (\(\mathrm{46\%}\) of the median), which is a notable outlier to the general upward salary-satisfaction trend. The employee with the median salary (\(\mathrm{100\%}\) of median) has a job satisfaction of \(\mathrm{60}\), which is above the median satisfaction value. In general, there is a positive correlation between salary and job satisfaction among the employees.
Step-by-Step Solution
Question 1: Median Job Satisfaction Employee's Salary
Complete Statement:
The employee having the median job satisfaction rating had a salary [BLANK] the median salary.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: employee having the median job satisfaction rating
- Meaning: Identify the employee whose job satisfaction rating sits at the median (the 6th value out of 11 when ordered lowest to highest).
- Relation to Chart: The x-axis lists job satisfaction ratings; the person with the middle (6th) highest rating is the median.
- Important Implications: We must find the specific salary associated with this median satisfaction rating.
- Statement Breakdown 2:
- Key Phrase: had a salary [BLANK] the median salary
- Meaning: Compare the identified employee's salary with the overall median salary value.
- Relation to Chart: The y-axis shows employee salary as a % of the median salary; \(\mathrm{100\%}\) means 'median'.
- Important Implications: If the employee has a salary percentage less than \(\mathrm{100}\), it is 'less than' the median; more than \(\mathrm{100}\) is 'greater than' the median.
- What is needed: Is the salary of the employee with the median job satisfaction rating less than, equal to, or greater than the median salary?
Solution:
- Condensed Solution Implementation:
Find the employee with job satisfaction rating equal to the median (\(\mathrm{55}\)), then check that employee's salary percentage. - Necessary Data points:
The median job satisfaction rating is \(\mathrm{55}\), and the corresponding salary is \(\mathrm{46\%}\) of the median salary. - Calculations Estimations:
\(\mathrm{46\%}\) is less than \(\mathrm{100\%}\); so this employee's salary is less than the median salary. - Comparison to Answer Choices:
Among 'less than', 'equal to', and 'greater than', the answer is 'less than'.
FINAL ANSWER Blank 1: less than
Question 2: Median Salary Employee's Job Satisfaction
Complete Statement:
The employee having the median salary had a job satisfaction rating [BLANK] the median rating.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: employee having the median salary
- Meaning: Identify the employee whose salary is at the median level (\(\mathrm{100\%}\) of the median salary).
- Relation to Chart: On the y-axis, find the point where salary is \(\mathrm{100\%}\).
- Statement Breakdown 2:
- Key Phrase: had a job satisfaction rating [BLANK] the median rating
- Meaning: Compare this employee's satisfaction rating to the overall median satisfaction rating.
- Relation to Chart: The median job satisfaction is \(\mathrm{55}\) (as previously determined).
- What is needed: Is the job satisfaction of the employee with the median salary less than, equal to, or greater than the median satisfaction rating?
Solution:
- Condensed Solution Implementation:
Find the employee whose salary is exactly \(\mathrm{100\%}\) of the median, then check their job satisfaction rating. - Necessary Data points:
The median salary is \(\mathrm{100\%}\); the corresponding job satisfaction is \(\mathrm{60}\). - Calculations Estimations:
\(\mathrm{60}\) is greater than \(\mathrm{55}\); so this employee's satisfaction is greater than the median. - Comparison to Answer Choices:
Among 'less than', 'equal to', and 'greater than', the answer is 'greater than'.
FINAL ANSWER Blank 2: greater than
Summary
The employee with the median job satisfaction rating (\(\mathrm{55}\)) has a salary much less than the median (\(\mathrm{46\%}\)), while the employee with the median salary (\(\mathrm{100\%}\)) has a job satisfaction higher than the median (\(\mathrm{60}\)). This highlights that the two medians do not necessarily correspond to the same employee or comparable values in the dataset.
Question Independence Analysis
The two questions are independent: each requires finding a different employee (median satisfaction vs. median salary) and comparing different attributes. While both deal with medians, solving one does not directly affect the other.