For each of four voting districts (Districts 1 through 4), the graph shows the percent of the voters in that...
GMAT Graphics Interpretation : (GI) Questions
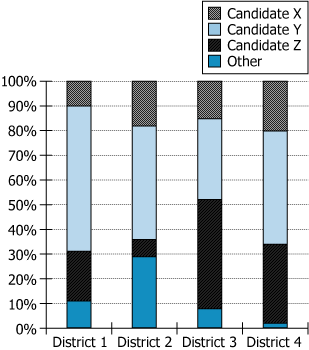
For each of four voting districts (Districts 1 through 4), the graph shows the percent of the voters in that district who voted for each of the three major candidates (Candidates X, Y, and Z) for mayor of a certain town, and the percent who voted for a candidate other than these three.
Select from the drop-down menus the options that create the most accurate statement based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Number of districts | For each of four voting districts (Districts 1 through 4) | There are four voting districts being analyzed |
| Focus of graph | the graph shows the percent of the voters in that district who voted for each of the three major candidates | The chart breaks down what share of voters chose each major candidate |
| Candidates named | (Candidates X, Y, and Z) | The three main candidates are labeled X, Y, and Z |
| Voting for others | and the percent who voted for a candidate other than these three | Some voters picked minor (non-major) candidates as well |
Table 2: Chart Analysis
| Chart Component | What's Shown | What This Tells Us |
|---|---|---|
| Chart type | Stacked bar chart with 4 categories (Districts 1-4) | Each district's results are represented as a stack adding up to \\(100\%\\) |
| Y-axis | Percentage scale from \\(0\%\\) to \\(100\%\\) | Each section reflects what proportion of the district's votes went to whom |
| Segment order/colors | Segments for 'Other', Z, Y, and X (percentages shown for each within each bar) | It's easy to visually compare sizes (percentages) between candidates/districts |
| Notable bar findings | District 2 has the lowest Candidate Z (\\(7\%\\)), District 4 has much higher Candidate Z (\\(32\%\\)) | Candidate Z is over 4 times as popular in District 4 vs. District 2 |
Key Insights
District 4's support for Candidate Z (\\(32\%\\)) is more than three times that in District 2 (\\(7\%\\)), which is the only combination to meet the 'three times' threshold described. Candidate Y is strong in all districts except District 3, where Candidate Z leads. Support for 'Other' candidates varies significantly, from high in District 2 (\\(29\%\\)) to very low in District 4 (\\(2\%\\)).
Step-by-Step Solution
Question 1: Identifying the Comparison District
Complete Statement:
Voters in District 4 were more than three times as likely as voters in District [BLANK 1] to have voted for Candidate [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: Voters in District 4
Meaning: District 4 is the main group being compared in the statement.
Relation to Chart: We need to look up District 4's voting percentages for all candidates.
Important Implications: Every comparison uses District 4's voting percentages as the numerator.
- Key Phrase: Voters in District 4
- Statement Breakdown 2:
- Key Phrase: more than three times as likely
Meaning: The ratio of District 4's percentage to another district's must be greater than 3.
Relation to Chart: We compare District 4's percentage for a candidate to other districts' percentages for the same candidate.
Important Implications: Only pairs with a ratio greater than 3 qualify. We must do this check for all candidates and possible districts.
- Key Phrase: more than three times as likely
What is needed: Which other district (1, 2, or 3), when compared to District 4, and for some candidate, has a vote percentage such that District 4's is more than three times higher.
Solution:
- Condensed Solution Implementation:
Check each candidate's percentage in District 4 and compare it to their percentage in Districts 1, 2, and 3 to find an instance where District 4's is more than three times greater. - Necessary Data points:
Candidate Z: District 1 (\\(20\%\\)), District 2 (\\(7\%\\)), District 3 (\\(44\%\\)), District 4 (\\(32\%\\))- Calculations Estimations:
District 4 vs District 1 for Z: \\(\\frac{32\%}{20\%} = 1.6\\); District 4 vs District 2 for Z: \\(\\frac{32\%}{7\%} \\approx 4.57\\); District 4 vs District 3 for Z: \\(\\frac{32\%}{44\%} \\approx 0.73\\). Only District 2 meets the ratio \\(\\gt 3\\) condition. - Comparison to Answer Choices:
Compared all options; only District 2 produces a ratio greater than 3 for any candidate.
- Calculations Estimations:
FINAL ANSWER Blank 1: 2
Question 2: Identifying the Candidate
Complete Statement:
Voters in District 4 were more than three times as likely as voters in District 2 to have voted for Candidate [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: to have voted for Candidate [BLANK 2]
Meaning: Find which candidate's voting percentages in District 4 and District 2 create a ratio greater than 3.
Relation to Chart: Review Candidate X, Y, and Z's percentages for Districts 4 and 2 and compute ratio.
- Key Phrase: to have voted for Candidate [BLANK 2]
What is needed: Which candidate's percentage for District 4 is more than three times District 2's percentage.
Solution:
- Condensed Solution Implementation:
For candidates X, Y, and Z, compare their support in Districts 4 and 2. Find candidate where District 4's percentage is more than three times that of District 2. - Necessary Data points:
Candidate X: District 4 (\\(20\%\\)), District 2 (\\(18\%\\)); Candidate Y: District 4 (\\(46\%\\)), District 2 (\\(46\%\\)); Candidate Z: District 4 (\\(32\%\\)), District 2 (\\(7\%\\))- Calculations Estimations:
For X: \\(\\frac{20\%}{18\%} \\approx 1.11\\); for Y: \\(\\frac{46\%}{46\%} = 1\\); for Z: \\(\\frac{32\%}{7\%} \\approx 4.57\\). - Comparison to Answer Choices:
Candidate Z is the only choice producing the required ratio \\(\\gt 3\\).
- Calculations Estimations:
FINAL ANSWER Blank 2: Z
Summary
For the statement to be true, District 4 must have a candidate whose support is more than three times that of another district for the same candidate. Only Candidate Z and District 2 meet this condition, with \\(32\%\\) support in District 4 and \\(7\%\\) in District 2, giving a ratio of approximately \\(4.57\\).
Question Independence Analysis
The blanks are dependent: identifying the correct district depends on the candidate, and vice versa. The solution emerges only when both are found to satisfy the required ratio together.