For each of four symptoms, the graph shows the percentage chances that someone will have that symptom on each day...
GMAT Graphics Interpretation : (GI) Questions
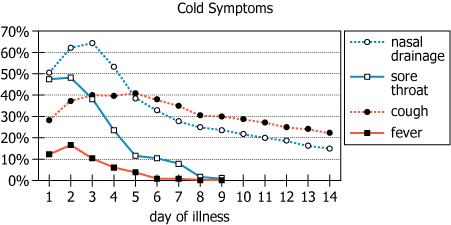
For each of four symptoms, the graph shows the percentage chances that someone will have that symptom on each day of the 2 weeks after first developing a cold. The lines for certain symptoms do not continue past a certain day because the chance that someone will have those symptoms beyond that day is less than 1%.
Select the options from the drop-down menus that create the statement that is most strongly supported by the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Subject Matter | For each of four symptoms | Tracks four symptoms: nasal drainage, sore throat, cough, fever |
| Data Expression | percentage chances that someone will have that symptom | Probability (as percent) someone has each symptom |
| Time Span | each day of the 2 weeks after first developing a cold | Daily data for 14 days post-onset |
| Data Limitation | lines for certain symptoms do not continue past a certain day because the chance...is \(\lt 1\%\) | Chart omits data when chance drops below \(1\%\) |
Table 2: Chart Analysis
| Chart Component | What is Displayed | Interpretation |
|---|---|---|
| Chart Type | Line chart with four symptom series over days 1-14 | Visualizes probability trends for each symptom over cold duration |
| X-axis | Days after first cold symptoms (1-14) | Time progression: daily view for two weeks after initial symptoms |
| Y-axis | Percentage (0-70%) | Shows likelihood as percent; max probability for symptoms \(\lt 70\%\) |
| Symptom Series | Nasal drainage, sore throat, cough, fever | Each symptom shown separately for comparison |
| Line Disappearance | Lines for sore throat and fever end before day 14 | Their probability drops below \(1\%\), so not shown after that day |
| Persistence | Nasal drainage & cough persist longest; fever disappears first | Persistence and duration of symptoms vary; fever resolves most rapidly |
Key Insights
After examining the text and the chart, we see that most symptoms decrease quickly in probability over time, but nasal drainage and cough are most likely to persist throughout the two-week period, while sore throat and especially fever typically resolve within the first week. The dataset uses a \(1\%\) probability threshold, so lines end once probabilities are negligible, clearly showing main symptom durations. By around day 10, only nasal drainage and cough remain above the threshold, so the chance someone has more than two symptoms by then is exceedingly low.
Step-by-Step Solution
Question 1: Determining How Many Symptoms Remain with High Probability
Complete Statement:
It can be determined from the graph that the probability is greater than \(0.98\) that someone with a cold will have [BLANK 1] of the four symptoms on day [BLANK 2].
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: probability is greater than \(0.98\)
Meaning: We are seeking information that is almost certain, with more than a \(98\%\) chance.
Relation to Chart: This requires finding moments on the chart when the presence or absence of symptoms can be predicted with high certainty.
Important Implications: We should focus on when symptom probabilities are so low or high that there is almost no uncertainty.
Statement Breakdown 2:
- Key Phrase: someone with a cold will have [BLANK 1] of the four symptoms
Meaning: We need the number of symptoms a sick person is likely to have, of these four: nasal drainage, sore throat, cough, fever.
Relation to Chart: The chart tracks the probability for each of the four symptoms over 14 days.
Important Implications: If one or more of these symptoms disappears (probability approaches zero), we are limited in how many symptoms a person can have.
What is needed: The highest number of symptoms that a person can have on the specified day with greater than \(98\%\) certainty.
Solution:
Condensed Solution Implementation:
Check the probabilities of each symptom on the days shown. When only two symptoms remain above the threshold, and the other two are almost never present, the probability that someone has more than two symptoms is very close to 0. This means it is almost certain (probability \(\gt 0.98\)) that a person will have two or fewer symptoms.
Necessary Data points:
On day 10, nasal drainage is about \(22\%\) and cough about \(29\%\). Sore throat and fever have both dropped below \(1\%\) probability (the chart lines disappear at this point).
Calculations Estimations:
Because sore throat and fever have dropped below \(1\%\) chance, almost no one will have either. Therefore, the most symptoms someone can have is two (nasal drainage and/or cough). The probability someone has more than two symptoms is practically zero, so the probability of 'two or fewer' is over \(98\%\).
Comparison to Answer Choices:
"One or fewer" is too restrictive (since up to two symptoms are possible). "One or more" doesn't restrict enough. "Exactly two" is too specific, since a person might have one or zero symptoms. "Two or fewer" matches: probability \(\gt 0.98\) that someone will have this many symptoms.
FINAL ANSWER Blank 1: Two or fewer
Question 2: Which Day Matches the High-Probability Symptom Limit
Complete Statement:
It can be determined from the graph that the probability is greater than \(0.98\) that someone with a cold will have two or fewer of the four symptoms on day [BLANK 2].
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: two or fewer of the four symptoms on day [BLANK 2]
Meaning: We need to find out on which day it's almost certain that someone with a cold has at most two symptoms.
Relation to Chart: This will occur when two symptoms have fallen below the probability threshold (almost never seen), leaving only two possible.
What is needed: The first day where it becomes virtually certain that a person with a cold will have no more than two symptoms.
Solution:
Condensed Solution Implementation:
Look for the day when cough and nasal drainage are the only symptoms remaining above the \(1\%\) probability line; sore throat and fever are no longer visible on the chart at that point.
Necessary Data points:
Day 10: Only nasal drainage (\(22\%\)) and cough (\(29\%\)) remain. Sore throat and fever are both below \(1\%\) probability.
Calculations Estimations:
On day 2, all four symptoms are likely possible. On day 6, fever is just dropping to \(1\%\), others are still present. On day 10, only two symptoms have any notable chance. So, on day 10, probability is \(\gt 0.98\) that someone will have at most two symptoms.
Comparison to Answer Choices:
Day 2 (too early), Day 6 (fever still possible), Day 10 (matches the number of symptoms possible). Thus, the correct answer is day 10.
FINAL ANSWER Blank 2: 10
Summary
By checking the symptom probabilities over time, we see that by day 10, only nasal drainage and cough remain. This means the chance of having more than two symptoms is less than \(2\%\). Therefore, someone with a cold is almost certain (\(\gt 98\%\)) to have two or fewer symptoms on day 10.
Question Independence Analysis
The answers are dependent: the number of symptoms is tied to the day, since symptoms drop off at different rates. Only on the correct day (day 10) can we be sure that two or fewer symptoms remain with probability above \(0.98\).