For a recent workday, the graph displays the round-trip distance and mode of travel for all persons travelling to work...
GMAT Graphics Interpretation : (GI) Questions
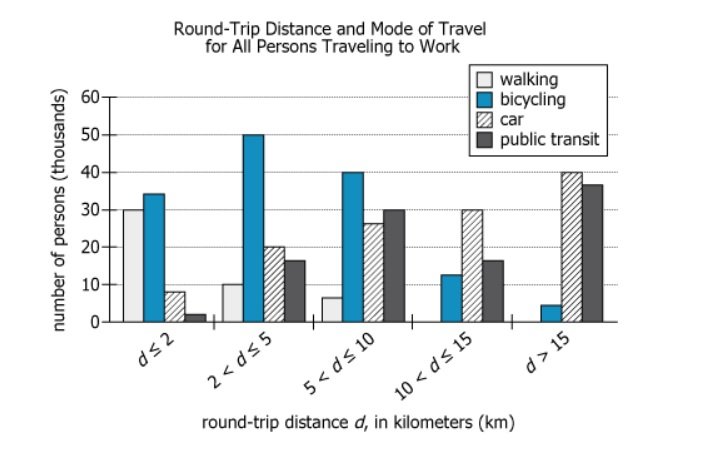
For a recent workday, the graph displays the round-trip distance and mode of travel for all persons travelling to work in a medium-sized city.
From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Component | Content | Interpretation |
|---|---|---|
| Time frame | For a recent workday | Data refers to one typical workday |
| Population | All persons travelling to work | Covers every commuter in the city |
| Location | In a medium-sized city | Data is for one mid-sized urban area |
| Data measured | Round-trip distance and mode of travel | Shows how far people travel and which transport mode they use |
Table 2: Chart Analysis
| Component | Details | What it Shows |
|---|---|---|
| Chart type | Grouped bar chart, 5 distance categories, 4 travel modes | Compares transport mode usage by distance |
| X-axis | Distance bins: \(\mathrm{d≤2}\) km, \(\mathrm{2\lt d≤5}\) km, \(\mathrm{5\lt d≤10}\) km, \(\mathrm{10\lt d≤15}\) km, \(\mathrm{d\gt 15}\) km | Categories of cumulative round-trip distances |
| Y-axis | Number of persons (in thousands), up to 60k | Number of commuters per mode/distance |
| Mode: Walking | Peaks at \(\mathrm{d≤2}\) km (~30k), drops sharply after | Walking mainly used for very short trips |
| Mode: Bicycling | Max at \(\mathrm{2\lt d≤5}\) km (~50k), lower at all other distances | Bicycling most viable for short-to-medium commutes |
| Mode: Car | Low at \(\mathrm{d≤2}\) km, increases steadily, peaks at \(\mathrm{d\gt 15}\) km (~40k) | Car use rises with distance |
| Mode: Public transit | Increases with distance, low at \(\mathrm{d≤2}\) km, peaks at \(\mathrm{d\gt 15}\) km (~36k), sizable at \(\mathrm{5\lt d≤15}\) | Transit preferred for longer distances |
Key Insights
- Most people walk only for very short commutes: over half of all walkers travel 2 km or less round-trip, placing the walking median in the \(\mathrm{d≤2}\) km category.
- Public transit is used for longer commutes: over half of public transit users travel more than 10 km, with the median in the \(\mathrm{10\lt d≤15}\) km category.
- There is a sharp transition in transport mode by distance: walking quickly becomes negligible beyond 5 km, while public transit and car use dominate longer trips.
- Each mode has a preferred distance: walking for shortest, bicycling for medium-short, and car/transit for long commutes.
Step-by-Step Solution
Question 1: Walking Median Distance
Complete Statement:
For all persons who travelled to work by walking, the median round-trip distance (x), in kilometres, satisfies the inequality ______.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: all persons who travelled to work by walking
_ Meaning: Focuses only on those who went to work by walking.
_ Relation to Chart: Use only the data for the 'walking' category in the chart.
_ Important Implications: Ignore data for other transportation modes; only counts for walking matter.
- Key Phrase: all persons who travelled to work by walking
- Statement Breakdown 2:
- Key Phrase: median round-trip distance (x)
_ Meaning: The middle distance when all walking commuters are ordered from smallest to largest round-trip distance.
_ Relation to Chart: We will determine which category contains the median walker by cumulative totals.
_ Important Implications: Median for an even number of people is the average of the two middle values.
- Key Phrase: median round-trip distance (x)
What is needed: Which round-trip distance category contains the median walking commuter.
Solution:
- Condensed Solution Implementation:
Sum the number of walking commuters by category. Find which category contains the 23rd and 24th persons (since there are 46 in total and the median is between the 23rd and 24th). - Necessary Data points:
Walking: 30 (\(\mathrm{d≤2}\)), 10 (\(\mathrm{2\lt d≤5}\)), 6 (\(\mathrm{5\lt d≤10}\)), 0 (\(\mathrm{10\lt d≤15}\)), 0 (\(\mathrm{d\gt 15}\)); total = 46 (all numbers in thousands).
_ Calculations Estimations:
The first category (\(\mathrm{d≤2}\)) has 30, so both the 23rd and 24th median positions are included here. Therefore, the median falls within \(\mathrm{d≤2}\).
_ Comparison to Answer Choices:
The correct choice is \(\mathrm{x≤2}\).
FINAL ANSWER Blank 1: \(\mathrm{x≤2}\)
Question 2: Public Transit Median Distance
Complete Statement:
For all persons who travelled to work by public transit, the median round-trip distance (x), in kilometres, satisfies the inequality ______.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: all persons who travelled to work by public transit
_ Meaning: Focuses only on those who used public transit.
_ Relation to Chart: Use only the data for public transit from the chart.
- Key Phrase: all persons who travelled to work by public transit
- Statement Breakdown 2:
- Key Phrase: median round-trip distance (x)
_ Meaning: The middle distance among all public transit commuters, ordered by distance.
_ Relation to Chart: Determine which category contains the 51st person, since there are 101 in total.
- Key Phrase: median round-trip distance (x)
What is needed: Which round-trip distance category contains the median public transit commuter.
Solution:
- Condensed Solution Implementation:
Sum the number of public transit commuters by category. The median is the 51st person out of 101. - Necessary Data points:
Public Transit: 3 (\(\mathrm{d≤2}\)), 16 (\(\mathrm{2\lt d≤5}\)), 30 (\(\mathrm{5\lt d≤10}\)), 16 (\(\mathrm{10\lt d≤15}\)), 36 (\(\mathrm{d\gt 15}\)); total = 101 (all numbers in thousands).
_ Calculations Estimations:
Cumulative count up to \(\mathrm{d≤2}\): 3. Up to \(\mathrm{2\lt d≤5}\): 19. Up to \(\mathrm{5\lt d≤10}\): 49. Up to \(\mathrm{10\lt d≤15}\): 65. The 51st person falls in the \(\mathrm{10\lt d≤15}\) category.
_ Comparison to Answer Choices:
The correct choice is \(\mathrm{10\lt x≤15}\).
FINAL ANSWER Blank 2: \(\mathrm{10\lt x≤15}\)
Summary
For walking, the median is in the shortest distance category (\(\mathrm{x≤2}\) km) because more than half the walkers travel very short distances. For public transit, the median is in the \(\mathrm{10\lt x≤15}\) km range, reflecting transit's role for longer commutes. Calculating cumulative totals pinpoints the correct median category for each group.
Question Independence Analysis
The two questions are independent because each concerns a separate mode of transportation and uses distinct data from the chart.