For a given city, the graph represents the daily deviation, in degrees Fahrenheit (°F), of the high temperature from the...
GMAT Graphics Interpretation : (GI) Questions
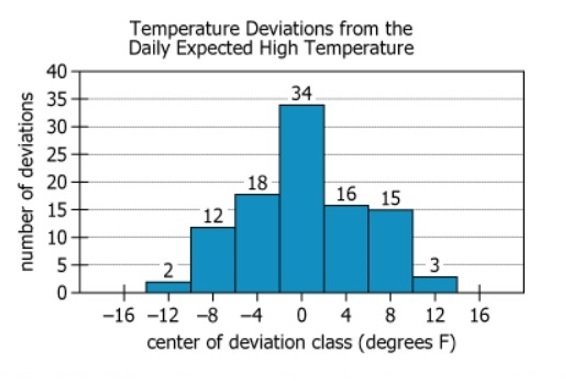
For a given city, the graph represents the daily deviation, in degrees Fahrenheit (\(°\mathrm{F}\)), of the high temperature from the expected high temperature for each day in a 100-day period. Data is grouped into disjoint classes of deviations: for each value of T marked on the horizontal axis, the class centered at T includes all observed deviations greater than or equal to \((\mathrm{T}-2)°\mathrm{F}\) but less than \((\mathrm{T}+2)°\mathrm{F}\). The height of each bar represents the number of deviations in the corresponding class. A given day's high temperature is \(\mathrm{x}°\mathrm{F}\) less than seasonal if it is \(\mathrm{x}°\mathrm{F}\) less than the left endpoint of the class centered at \(0\), and the high temperature is \(\mathrm{x}°\mathrm{F}\) greater than seasonal if it is \(\mathrm{x}°\mathrm{F}\) greater than the right endpoint of the class centered at \(0\).
From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Subject Matter | daily deviation, in degrees Fahrenheit (\(\mathrm{°F}\)), of the high temperature from the expected high temperature | Measures how high temperatures differed from the expected each day |
| Geographic Context | For a given city | Data is for one unnamed city |
| Time Period | 100-day period | Data covers exactly 100 consecutive days |
| Data Grouping Method | Data is grouped into disjoint classes of deviations | Deviations are grouped into separate bins without overlap |
| Class Definition | For each value of T on the horizontal axis, the class centered at T includes all observed deviations \(\geq \mathrm{(T-2)°F}\) but \(< \mathrm{(T+2)°F}\) | Each group spans \(\mathrm{4°F}\), centered on T |
| Bar Height Meaning | The height of each bar represents the number of deviations in the corresponding class | Taller bars mean more days with that range of deviation |
| "Less than seasonal" definition | If a day's high is \(\mathrm{x°F}\) less than the left endpoint of the class centered at 0 | Means \(\mathrm{x°F}\) below \(\mathrm{-2°F}\) |
| "Greater than seasonal" definition | If a day's high is \(\mathrm{x°F}\) greater than the right endpoint of the class centered at 0 | Means \(\mathrm{x°F}\) above \(\mathrm{+2°F}\) |
Table 2: Chart Analysis
| Chart Component | What's Shown | Meaning |
|---|---|---|
| Chart Type | Histogram (bar chart) | Distribution of temperature deviation counts |
| X-axis | Deviation class centers: -12, -8, -4, 0, 4, 8, 12 | Center of \(\mathrm{4°F}\)-wide bins, range from \(\mathrm{-14°F}\) to \(\mathrm{+14°F}\) |
| Y-axis | Number of deviations (up to 40) | For each bin, indicates how many days' highs fell in that deviation range |
| Bars (Heights) | -12: 2, -8: 12, -4: 18, 0: 34, 4: 16, 8: 15, 12: 3 | Most days clustered at \(\mathrm{0°F}\) (center); very few extreme deviations |
| Distribution | Bell-shaped, centered at \(\mathrm{0°F}\) | Typical high temperatures usually close to the expected, few outliers |
| Total Days | Sum = 100 | Accounts for all days in the period |
Key Insights
The majority of days (34 out of 100) had a high temperature within \(\pm\mathrm{2°F}\) of the expected value, as shown by the tallest central bar. There is a noticeable cold skew: 32 days (bars at -4, -8, -12) had highs at least \(\mathrm{2°F}\) colder than expected, whereas only 15 + 3 = 18 days (bars at 8, 12) had highs at least \(\mathrm{6°F}\) above expected. The data forms a normal-like (bell) distribution, with most values near \(\mathrm{0°F}\) deviation and quickly decreasing frequency for larger deviations. The definition of deviation bins and class endpoints is crucial for interpreting which days are counted as 'more than \(\mathrm{x°F}\) less/greater than seasonal.' No days exceeded \(\pm\mathrm{14°F}\) deviation.
Step-by-Step Solution
Question 1: Probability of High Temperature More Than \(\mathrm{4°F}\) Below Seasonal
Complete Statement:
For a randomly selected day in this 100-day period, the probability that the high temperature was more than \(\mathrm{4°F}\) less than seasonal is ______
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: randomly selected day in this 100-day period
- Meaning: We're asked to calculate the probability out of all 100 days represented.
- Relation to Chart: The chart's total is 100 days; each bar represents a number of days.
- Important Implications: The denominator for probability is 100.
- Statement Breakdown 2:
- Key Phrase: more than \(\mathrm{4°F}\) less than seasonal
- Meaning: We seek days where the deviation is more than \(\mathrm{4°F}\) below seasonal.
- Relation to Chart: Seasonal is set at the left endpoint of the class centered at \(\mathrm{0°F}\), which is \(\mathrm{-2°F}\). So, more than \(\mathrm{4°F}\) less means less than \(\mathrm{-6°F}\) (\(\mathrm{-2°F - 4°F = -6°F}\)).
- Important Implications: We need to count days where the temperature deviation is less than \(\mathrm{-6°F}\).
What is needed: The proportion of days with temperature deviations less than \(\mathrm{-6°F}\) (colder than \(\mathrm{-6°F}\)), out of 100.
Solution:
- Condensed Solution Implementation:
Examine the histogram classes to find the total number of days where deviations are less than \(\mathrm{-6°F}\). - Necessary Data points:
Class centered at \(\mathrm{-8°F}\) (range: \(\mathrm{-10°F}\) to \(\mathrm{-6°F}\)) has 12 days; class centered at \(\mathrm{-12°F}\) (range: \(\mathrm{-14°F}\) to \(\mathrm{-10°F}\)) has 2 days.- Calculations Estimations:
Total days = 12 (from \(\mathrm{-8°F}\) class) + 2 (from \(\mathrm{-12°F}\) class) = 14 days. Probability = \(\mathrm{\frac{14}{100} = 0.14}\). - Comparison to Answer Choices:
The answer 0.14 matches one of the provided choices.
- Calculations Estimations:
FINAL ANSWER Blank 1: 0.14
Question 2: Probability of High Temperature More Than \(\mathrm{8°F}\) Below Seasonal
Complete Statement:
and the probability that the high temperature was more than \(\mathrm{8°F}\) less than seasonal is ______
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: more than \(\mathrm{8°F}\) less than seasonal
- Meaning: We seek days where the deviation from seasonal is greater than \(\mathrm{8°F}\) (colder by more than \(\mathrm{8°F}\)).
- Relation to Chart: Seasonal is \(\mathrm{-2°F}\), so we look for deviations less than \(\mathrm{-10°F}\) (\(\mathrm{-2°F - 8°F = -10°F}\)).
What is needed: The proportion of days with temperature deviations less than \(\mathrm{-10°F}\) out of 100 days.
Solution:
- Condensed Solution Implementation:
Identify which histogram class includes values less than \(\mathrm{-10°F}\) and how many days are in that range. - Necessary Data points:
Class centered at \(\mathrm{-12°F}\) (range: \(\mathrm{-14°F}\) to \(\mathrm{-10°F}\)) has 2 days.- Calculations Estimations:
Only 2 days qualify. Probability = \(\mathrm{\frac{2}{100} = 0.02}\). - Comparison to Answer Choices:
The answer 0.02 matches one of the provided choices.
- Calculations Estimations:
FINAL ANSWER Blank 2: 0.02
Summary
For both blanks, determine where 'seasonal' is on the chart (at \(\mathrm{-2°F}\)), then subtract the given number (\(\mathrm{4°F}\) and \(\mathrm{8°F}\)) to set the cutoff. Count the days in the relevant classes that fall below the threshold, divide by 100, and select the matching answer. Answers: 0.14 and 0.02.
Question Independence Analysis
Each blank asks about temperatures with a different deviation below 'seasonal', and does not depend on the others. They both use the same method and data, but each answer stands alone.