For a given city, the graph represents the daily deviation, in °F, of the high temperature from the expected high...
GMAT Graphics Interpretation : (GI) Questions
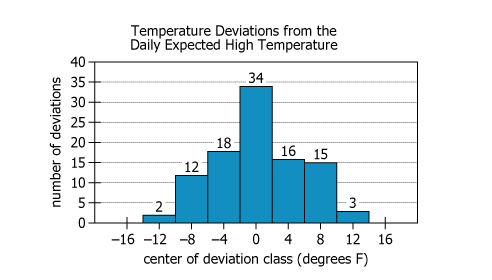
For a given city, the graph represents the daily deviation, in \(°\mathrm{F}\), of the high temperature from the expected high temperature for each day in a 100-day period. Data is grouped into disjoint classes of deviations: for each value of T marked on the horizontal axis, the class centered at T includes all observed deviations greater than or equal to \((T-2)°\mathrm{F}\) but less than \((T+2)°\mathrm{F}\). The height of each bar represents the number of deviations in the corresponding class. A given day's high temperature is \(x°\mathrm{F}\) less than seasonal if it is \(x°\mathrm{F}\) less than the left endpoint of the class centered at 0, and the high temperature is \(x°\mathrm{F}\) greater than seasonal if it is \(x°\mathrm{F}\) greater than the right endpoint of the class centered at 0.
From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Geographic Context | For a given city | Data applies to one specific (unnamed) city |
| Data Subject | Daily deviation...of the high temperature from expected | Shows how actual high temps differed daily |
| Time Period | 100-day period | Data spans 100 consecutive days |
| Class Definition | Class centered at T includes deviations \(\geq \mathrm{T}-2°\mathrm{F}\) and \(< \mathrm{T}+2°\mathrm{F}\) | Each bar covers a \(4°\mathrm{F}\)-wide range of deviations |
| Bar Height Meaning | Height of each bar = number of deviations in class | Bar height represents days in that deviation range |
| 'Less than seasonal' | \(x°\mathrm{F}\) less than seasonal = \(x°\mathrm{F}\) less than left endpoint of class centered at 0 | 'Less than seasonal' means colder than \(-2°\mathrm{F}\) deviation |
| 'Greater than seasonal' | \(x°\mathrm{F}\) greater than seasonal = \(x°\mathrm{F}\) greater than right endpoint of class centered at 0 | 'Greater than seasonal' means warmer than \(+2°\mathrm{F}\) deviation |
Table 2: Chart Analysis
| Chart Component | What's Shown | Interpretation |
|---|---|---|
| Chart Type | Histogram with 7 bars | Shows frequency of deviations across ranges |
| X-axis | Deviation class center values, from \(-12°\mathrm{F}\) to \(+12°\mathrm{F}\) | Measures degree difference from seasonal expectations |
| Y-axis | Number of days (frequency), from 0 to 40 | Indicates how many days per deviation range |
| Data Values | Bars: 2 (\(-12°\mathrm{F}\)), 12 (\(-8°\mathrm{F}\)), 18 (\(-4°\mathrm{F}\)), 34 (\(0°\mathrm{F}\)), 16 (\(+4°\mathrm{F}\)), 15 (\(+8°\mathrm{F}\)), 3 (\(+12°\mathrm{F}\)) | Most days clustered around expected temp (\(0°\mathrm{F}\)), few extremes |
| Peak | Highest bar: \(0°\mathrm{F}\) class with 34 days | Most highs were within \(2°\mathrm{F}\) of expected |
| Distribution | Approx. bell-shaped, symmetric about \(0°\mathrm{F}\) | Deviations follow a typical variation pattern |
Key Insights
- The majority of days (34 of 100) had high temperatures within \(\pm 2°\mathrm{F}\) of the expected seasonal value.
- Only 18 days (15 at \(+8°\mathrm{F}\), 3 at \(+12°\mathrm{F}\)) had high temperatures at least \(6°\mathrm{F}\) above expected (i.e., at least \(4°\mathrm{F}\) greater than seasonal).
- The temperature deviations are distributed symmetrically and in a bell-shaped pattern, with relatively few extreme outliers.
- All 100 days are accounted for by the data, confirming completeness of coverage.
Step-by-Step Solution
Question 1: Probability of High Temperature at Least 4°F Greater Than Seasonal
Complete Statement:
For a randomly selected day in this 100-day period, the probability that the high temperature was at least \(4°\mathrm{F}\) greater than seasonal is ________
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: randomly selected day in this 100-day period
- Meaning: We're asked for the probability over all 100 days shown in the histogram.
- Relation to Chart: All bars in the histogram together represent the 100 total days.
- Important Implications: Probability will be (number of favorable days) divided by 100.
- Key Phrase: randomly selected day in this 100-day period
- Statement Breakdown 2:
- Key Phrase: at least \(4°\mathrm{F}\) greater than seasonal
- Meaning: The temperature has to be at least \(4°\mathrm{F}\) above what counts as 'seasonal.'
- Relation to Chart: According to the setup, 'greater than seasonal' means above the right endpoint (\(2°\mathrm{F}\)) of the class centered at 0. So 'at least \(4°\mathrm{F}\) greater than seasonal' means at least \((2+4) = 6°\mathrm{F}\) above expected.
- Important Implications: The only days that count are those with temperature deviations of \(6°\mathrm{F}\) or more above expected.
- Key Phrase: at least \(4°\mathrm{F}\) greater than seasonal
- What is needed: The fraction of days in the histogram with deviations of at least \(6°\mathrm{F}\) above expected.
Solution:
- Condensed Solution Implementation:
Find the histogram bars that represent deviations of \(6°\mathrm{F}\) or more (classes centered at \(8°\mathrm{F}\) and \(12°\mathrm{F}\)), sum their frequencies, and divide by 100. - Necessary Data points:
The bar for class centered at \(8°\mathrm{F}\) (\([6°\mathrm{F}, 10°\mathrm{F})\)) contains 15 days; the bar for class centered at \(12°\mathrm{F}\) (\([10°\mathrm{F}, 14°\mathrm{F})\)) contains 3 days.- Calculations Estimations:
15 days (\(8°\mathrm{F}\) bin) + 3 days (\(12°\mathrm{F}\) bin) = 18 days; Probability: \(\frac{18}{100} = 0.18\). - Comparison to Answer Choices:
The answer choices include 0.18. Our calculated probability matches this value.
- Calculations Estimations:
FINAL ANSWER Blank 1: 0.18
Question 2: Probability of High Temperature at Least 8°F Greater Than Seasonal
Complete Statement:
and the probability that the high temperature was at least \(8°\mathrm{F}\) greater than the seasonal is _______
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: at least \(8°\mathrm{F}\) greater than seasonal
- Meaning: The temperature has to be at least \(8°\mathrm{F}\) above what counts as 'seasonal.'
- Relation to Chart: Using the same logic as before, this means at least \((2+8) = 10°\mathrm{F}\) above expected.
- Key Phrase: at least \(8°\mathrm{F}\) greater than seasonal
- What is needed: The fraction of days in the histogram with deviations of at least \(10°\mathrm{F}\) above expected.
Solution:
- Condensed Solution Implementation:
Find the histogram bar(s) for deviations of \(10°\mathrm{F}\) or more (class centered at \(12°\mathrm{F}\) only), sum their frequencies, and divide by 100. - Necessary Data points:
The bar for class centered at \(12°\mathrm{F}\) (\([10°\mathrm{F}, 14°\mathrm{F})\)) contains 3 days.- Calculations Estimations:
3 days (\(12°\mathrm{F}\) bin); Probability: \(\frac{3}{100} = 0.03\). - Comparison to Answer Choices:
The answer choices include 0.03, agreeing with our calculation.
- Calculations Estimations:
FINAL ANSWER Blank 2: 0.03
Summary
By noting that '\(x°\mathrm{F}\) greater than seasonal' means \(x°\mathrm{F}\) above the right endpoint (\(2°\mathrm{F}\)) of the class centered at 0, we translate the worded description into a simple counting problem on the histogram. For at least \(4°\mathrm{F}\) above seasonal (i.e., \(\geq 6°\mathrm{F}\) above expected) there are 18 days (0.18 probability), and for at least \(8°\mathrm{F}\) above seasonal (i.e., \(\geq 10°\mathrm{F}\) above expected) there are 3 days (0.03 probability).
Question Independence Analysis
These questions are independent because each asks for the probability of a different temperature threshold above seasonal, and each is solved by counting the relevant days separately.