For a certain electronics retailer during each of eight days, both of the graphs show the number of televisions sold...
GMAT Graphics Interpretation : (GI) Questions
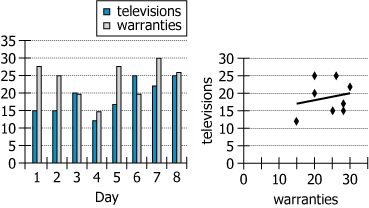
For a certain electronics retailer during each of eight days, both of the graphs show the number of televisions sold and the number of extended warranties sold (whether for televisions or for any other products sold at the store). The scatterplot also includes a trendline that shows the correlation between the daily numbers of televisions and warranties sold.
Select from the drop-down menus the options that complete the statement so that it is accurate based on the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Original Content | Interpretation |
|---|---|---|
| Subject | "For a certain electronics retailer" | The data is from one electronics store |
| Time Period | "during each of eight days" | Data covers 8 days |
| Metric 1 | "the number of televisions sold" | TVs sold per day |
| Metric 2 | "the number of extended warranties sold (whether for televisions or for any other products sold at the store)" | Warranties sold per day, including those for all products |
| Shown by | "both of the graphs show..." | Two different visualizations present the same underlying data |
| Additional Chart Feature | "The scatterplot also includes a trendline that shows the correlation..." | Charts not only present data but also highlight correlation |
Table 2: Chart Analysis
| Chart Component | Description | Observation |
|---|---|---|
| Chart Types | Grouped bar chart (left), Scatterplot with trendline (right) | Shows both daily data and overall relationship |
| Bar Chart | Two bars per day (one for TVs, one for warranties), shown for Days 1-8 | Allows direct daily comparison |
| Scatterplot Axes | X: warranties sold, Y: TVs sold | Each day's data plotted as a point |
| Trendline | Linear, shown on scatterplot | Indicates strength and direction of correlation |
| Variation | TVs: 12.5–25 per day; Warranties: 14.5–30 per day | Warranties have a wider range |
| Outlier Day | Day 6 (high TVs, low warranties) | Disrupts the general pattern seen in other days |
Key Insights
There is a general positive correlation between TVs and warranty sales, as indicated by the trendline on the scatterplot. However, certain days like Day 6 stand out as outliers: it has the highest number of TVs sold but only average warranty sales, weakening the overall trend. Warranty sales show more variability across days compared to TV sales. Both metrics reach their lowest values on Day 4 (12.5 TVs, 14.5 warranties), making it a low point for the period.
Step-by-Step Solution
Question 1: Identify the Outlier Day Impacting Correlation
Complete Statement:
Among the days represented in the graphs, without the data for Day [BLANK 1], the daily numbers of televisions and extended warranties sold would [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: Among the days represented in the graphs
_ Meaning: We are evaluating all the days shown in the visual data.
_ Relation to Chart: Refers to all days in both the bar graph and the scatterplot.
_ Important Implications: Every day presented can be chosen for blank 1, but only those offered as options are valid.
- Key Phrase: Among the days represented in the graphs
- Statement Breakdown 2:
- Key Phrase: without the data for Day [BLANK 1]
_ Meaning: We are being asked to consider the effect of deleting one day's data from the dataset.
_ Relation to Chart: This means removing a single dot from the scatterplot and one pair of bars from the bar chart.
_ Important Implications: The choice of which day to remove will change the apparent relationship between TV and warranty sales.
- Key Phrase: without the data for Day [BLANK 1]
What is needed: Which day, when removed, will most dramatically impact the direction or strength of the correlation between TV and warranty sales?
Solution:
- Condensed Solution Implementation:
Scan the chart for any day where the data is unusually different from the others. Identify which offered day acts as an outlier impacting correlation. - Necessary Data points:
Day 1: 15 TVs, 27.5 warranties; Day 4: 12.5 TVs, 14.5 warranties; Day 6: 25 TVs, 19.5 warranties.
_ Calculations Estimations:
Day 4's point is separated from the general trend—it combines the lowest TV sales with low warranties, making it an extreme value in the dataset. Removing it would eliminate this outlier.
_ Comparison to Answer Choices:
Day 4 is the offered day whose removal would most change the correlation. Days 1 and 6 are closer to the main data cluster and have less impact.
FINAL ANSWER Blank 1: 4
Question 2: Determine the Changed Correlation After Removing the Outlier
Complete Statement:
The daily numbers of televisions and extended warranties sold would [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: would [BLANK 2]
_ Meaning: We must describe how the relationship between TV and warranty sales changes after removing Day 4.
_ Relation to Chart: This means the trendline in the scatterplot may change—either becoming weaker or reversing direction.
- Key Phrase: would [BLANK 2]
What is needed: How will the removal of Day 4's data affect the overall correlation between TV and warranty sales?
Solution:
- Condensed Solution Implementation:
Consider whether the positive correlation visible is due to Day 4's data point. Visualize the scatterplot without Day 4 to judge the impact. - Necessary Data points:
Day 4's extremely low values set it apart as a critical driver of the current positive correlation.
_ Calculations Estimations:
Without Day 4, the remaining data points do not maintain the same trend. The pattern is much less clear, so the correlation likely disappears.
_ Comparison to Answer Choices:
The correct answer is the correlation would 'no longer be positively correlated' after removing Day 4.
FINAL ANSWER Blank 2: no longer be positively correlated
Summary
Removing Day 4, the outlier with both the lowest TV and warranty sales, causes the positive correlation between TV and warranty sales to disappear. Thus, Day 4 is essential for the trend seen across all days.
Question Independence Analysis
The two blanks are dependent: the answer to the second blank hinges directly on which day is removed in the first blank, since the effect on correlation depends on that choice.