Facts: The graph refers to a plane's flight from one location to another. The vertical axis represents the distance, in...
GMAT Graphics Interpretation : (GI) Questions
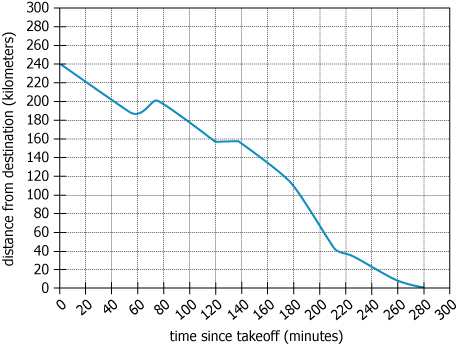
Facts: The graph refers to a plane's flight from one location to another. The vertical axis represents the distance, in kilometers, between the plane and its destination. The horizontal axis represents the time, t minutes, since takeoff.
Make the appropriate selection from each drop-down menu to complete each sentence so that it is consistent with the information presented in the graph.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Subject | The graph refers to a plane's flight from one location to another | This is about an airplane journey between two places |
| Y-axis | The vertical axis represents the distance, in kilometers, between the plane and its destination | Y-axis shows how far the plane is from its destination (in km) |
| X-axis | The horizontal axis represents the time, t minutes, since takeoff | X-axis shows minutes passed since takeoff |
Table 2: Chart Analysis
| Chart Part | Description | Interpretation |
|---|---|---|
| Chart Type | Single line graph | Flight progress shown over time |
| Y-axis Range | 0–300 kilometers, 20 km intervals | Plane starts about 240 km from arrival |
| X-axis Range | 0–300 minutes, 20 min intervals | Flight lasts about 5 hours |
| Line Trend | Decreasing, minor increase at 60–80 minutes | Mostly moving closer, one move away |
| Steepest Descent | 180–200 minutes | Fastest approach in this interval |
Key Insights
- The plane's distance from its destination mostly decreases, aligning with a typical flight trajectory.
- There is one unusual period (60–80 minutes) where the plane briefly increases its distance from the destination, suggesting an anomaly such as diversion or holding pattern.
- The flight's fastest progress toward the destination happens between 180 and 200 minutes, seen in the steepest drop in distance on the graph.
Step-by-Step Solution
Question 1: Comparison of Plane's Proximity to Destination at Two Times
Complete Statement:
The plane was closer to its destination at [BLANK 1]
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: closer to its destination
Meaning: We are being asked to determine at which of two times the plane was physically closer to its final destination.
Relation to Chart: This is measured by the y-axis value (distance from destination) — the lower the value, the closer the plane is.
Important Implications: A lower y-axis (distance) value at a given time point means the plane is closer to its destination.
- Key Phrase: closer to its destination
- Statement Breakdown 2:
- Key Phrase: at [BLANK 1]
Meaning: We're to choose which pair of times fits this description from among the dropdown options.
Relation to Chart: For each possible answer, we compare y-values at two different times as shown on the chart.
Important Implications: Normally, as time progresses, the plane gets closer to its destination, but we're being asked to notice if there is an exception to this trend.
- Key Phrase: at [BLANK 1]
- What is needed: The pair of times for which the earlier time showed the plane actually closer to its destination than the later time.
Solution:
- Condensed Solution Implementation:
Survey the chart for all given pairs of times. For each, compare the y-values (distances). Usually, the later time is closer, but we check carefully for any anomaly. - Necessary Data points:
Identify the y-values (distances from destination) at t = 60 and t = 80. At t = 60, the distance is about 190 km; at t = 80, the distance increases to about 200 km.
Calculations Estimations:
Since 190 km (at t = 60) < 200 km (at t = 80), the plane was closer at t = 60 than at t = 80. All other pairs follow the normal trend: the later time is closer.
Comparison to Answer Choices:
The only time pair matching the condition is 't = 60 than at t = 80'. This is the anomaly; all other options are not exceptions.
FINAL ANSWER Blank 1: t = 60 than at t = 80
Question 2: Greatest Progress Toward Destination in a 20-Minute Interval
Complete Statement:
Of all of the 20-minute intervals beginning and ending at times labeled on the graph, the interval in which the plane traveled farthest toward its destination was the interval from [BLANK 2]
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: 20-minute intervals beginning and ending at times labeled on the graph
Meaning: We're limited to intervals of exactly 20 minutes, starting and ending at times printed on the chart's x-axis.
Relation to Chart: We are to analyze the slope (drop) of the distance in each of those intervals.
- Key Phrase: 20-minute intervals beginning and ending at times labeled on the graph
- Statement Breakdown 2:
- Key Phrase: traveled farthest toward its destination
Meaning: We need to identify where the plane made the largest decrease in distance within one interval.
Relation to Chart: Look for the interval with the steepest downward slope on the graph.
- Key Phrase: traveled farthest toward its destination
- What is needed: Which 20-minute interval saw the largest drop (decrease) in distance to the destination.
Solution:
- Condensed Solution Implementation:
Visually check each eligible 20-minute interval on the graph and measure the change in distance (how much the y-value decreases). - Necessary Data points:
For t = 180 to t = 200, the distance drops from about 120 km to about 60 km, a change of about 60 km downward. Other intervals either have a smaller downward change or, in the case of t = 60 to t = 80, even an increase.
Calculations Estimations:
60 km reduction over the interval t = 180 to t = 200 is the largest downward movement among the options.
Comparison to Answer Choices:
No other 20-minute interval has as large a decrease. Thus, t = 180 to t = 200 is the answer.
FINAL ANSWER Blank 2: t = 180 to t = 200
Summary
To answer both questions, carefully read the graph. Question 1 required noticing the unusual increase in distance between t = 60 and t = 80, so the earlier time (t = 60) was closer. Question 2 is solved by finding the steepest drop in any 20-minute interval, which occurs from t = 180 to t = 200.
Question Independence Analysis
The two questions are independent. Question 1 asks about a detail in one time pair, while Question 2 looks for the greatest change over an interval. You can answer each without knowledge of the other.