Coworkers Fang, Gan, Hua, Ji, and Kun must complete three new projects: a brochure, a report, and a spreadsheet. Each...
GMAT Graphics Interpretation : (GI) Questions
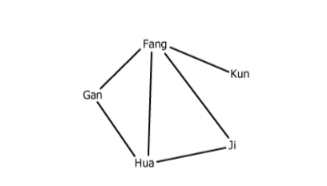
Coworkers Fang, Gan, Hua, Ji, and Kun must complete three new projects: a brochure, a report, and a spreadsheet. Each worker will work on exactly one of these projects. Exactly one worker—but not Hua—will work on the spreadsheet. The coworkers' manager will not assign any workers who are close friends to work together on a project. Lines in the graph connect two names if and only if the two Individuals are close friends.
Select from each drop-down menu the option that creates the most accurate statement, assuming the constraints described in the passage are adhered to.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Workers | "Coworkers Fang, Gan, Hua, Ji, and Kun" | Five workers to be assigned |
| Projects | "three new projects: a brochure, a report, and a spreadsheet" | There are three projects |
| Assignment constraint | "Each worker will work on exactly one of these projects" | Each worker gets only one project |
| Spreadsheet constraint | "Exactly one worker—but not Hua—will work on the spreadsheet" | The spreadsheet must have only one worker, and it cannot be Hua |
| Friendship constraint | "The coworkers' manager will not assign any workers who are close friends to work together on a project" | Friends cannot be on the same project |
| Graph explanation | "Lines in the graph connect two names if and only if the two individuals are close friends" | Lines in the chart show who is friends with whom |
Table 2: Chart Analysis
| Chart Component | Observation | Interpretation |
|---|---|---|
| Fang's connections | Fang is connected to Gan, Hua, Ji, Kun (all others) | Fang is friends with everyone, so cannot share a project |
| Kun's connections | Kun is only connected to Fang | Kun is only restricted from working with Fang |
| Other connections | Gan-Hua, Gan-Fang, Hua-Ji, Ji-Fang | Central group with multiple overlapping friendships |
| Nonfriend pairs | Gan-Ji, Gan-Kun, Hua-Kun, Ji-Kun | Only these pairs can work on the same project |
| Network type | Undirected graph | Friendship is mutual and matters equally for both sides |
Key Insights
- Fang is friends with everyone, so must be assigned alone to a project.
- Kun has only one friend, Fang, so is free to work with any of Gan, Hua, or Ji.
- The restriction that only one person (not Hua) can do the spreadsheet means Fang, Gan, Ji, or Kun must do it alone.
- Only four pairs among the workers are not friends (Gan-Ji, Gan-Kun, Hua-Kun, Ji-Kun), so possible teams are highly limited.
- Assigning projects thus depends on both these friendship constraints and the one-person spreadsheet rule.
Step-by-Step Solution
Question 1: Conditional Assignment to Brochure
Complete Statement:
[BLANK 1] could be assigned to work on the brochure, but only if Gan is assigned to work on the [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: [BLANK 1] could be assigned to work on the brochure
- Meaning: We're asked which worker's assignment to brochure is conditional.
- Relation to Chart: We have to consider friendship connections, since no close friends can be assigned to the same project.
- Important Implications: Some workers can only do brochure depending on where others are assigned due to friendship exclusions.
- Statement Breakdown 2:
- Key Phrase: but only if Gan is assigned to work on the [BLANK 2]
- Meaning: The assignment of [BLANK 1] is only possible for the brochure if Gan is assigned to a certain project.
- Relation to Chart: Gan's assignment will either allow or prevent [BLANK 1] from being assigned to brochure depending on their friendship status.
- Important Implications: We need to test each worker in [BLANK 1]'s spot and see which Gan assignment is critical for that worker to do brochure.
- What is needed: Which worker among Fang, Ji, or Kun could be assigned to the brochure, but only if Gan is assigned to a particular project.
Solution:
- Condensed Solution Implementation:
Check which pairings are allowed by the friendship graph. Fang cannot work with anyone else (friends with all), so their assignment is not conditional. Kun is only friends with Fang, so Kun and Gan can work together. However, the statement is constructed around the conditional nature, pointing to Ji and Gan, who are not friends and can be assigned together. - Necessary Data points:
Friendship pairs: Fang is friends with everyone. Ji is friends with Fang and Hua. Gan and Ji are NOT friends. Gan and Kun are NOT friends.- Calculations Estimations:
Check Ji on brochure: only allowed if Gan is also on brochure, since Ji and Gan are not friends and can both be on brochure without violating constraints. Ji's ability to be on brochure critically depends on Gan's assignment. - Comparison to Answer Choices:
Fang can't be with any other worker. Kun's assignment doesn't create a conditional restriction. Ji's only way onto brochure is if Gan is also assigned to brochure.
- Calculations Estimations:
FINAL ANSWER Blank 1: Ji
Question 2: Gan's Project Required for Ji on Brochure
Complete Statement:
Ji could be assigned to work on the brochure, but only if Gan is assigned to work on the [BLANK 2].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: Ji could be assigned to work on the brochure
- Meaning: Ji's assignment to brochure is under consideration.
- Relation to Chart: Possible as long as Ji doesn't have to work with a friend (Fang or Hua).
- Statement Breakdown 2:
- Key Phrase: but only if Gan is assigned to work on the [BLANK 2]
- Meaning: Gan's assignment is the key enabler for Ji's assignment.
- Relation to Chart: Ji and Gan are not friends, so they are allowed to work together on a project.
- What is needed: Which project Gan must be assigned to, in order for Ji to be able to work on the brochure.
Solution:
- Condensed Solution Implementation:
Since Gan and Ji are not friends, the only project Gan must be on to allow Ji on brochure is brochure itself. This is the only way Ji can work on brochure given the constraints. - Necessary Data points:
Gan and Ji are not friends, so a shared assignment is allowed.- Calculations Estimations:
Only if Gan is on brochure, Ji can also be on brochure. Other assignments for Gan do not enable Ji onto brochure. - Comparison to Answer Choices:
Possible Gan assignments are brochure, report, spreadsheet. Only brochure fits the required conditional for Ji.
- Calculations Estimations:
FINAL ANSWER Blank 2: brochure
Summary
Ji could be assigned to the brochure, but only if Gan is also assigned to the brochure. No such conditional applies for Fang or Kun; Fang cannot work with any co-worker, and Kun's assignment isn't conditional on Gan. The answer follows from the friendship graph and the exclusivity constraint: since Ji and Gan are not friends, they can be in the same assignment, allowing this conditional. Thus, the fill is 'Ji' and 'brochure'.
Question Independence Analysis
The blanks are dependent. Selecting Ji for Blank 1 establishes the relevant friendship and exclusivity constraints, making 'brochure' the unique suitable answer for Blank 2. Blank 2 cannot be determined without the answer to Blank 1.