Before deciding whether to accept a batch of grain, agricultural-import inspectors in a certain country test five samples from the...
GMAT Graphics Interpretation : (GI) Questions
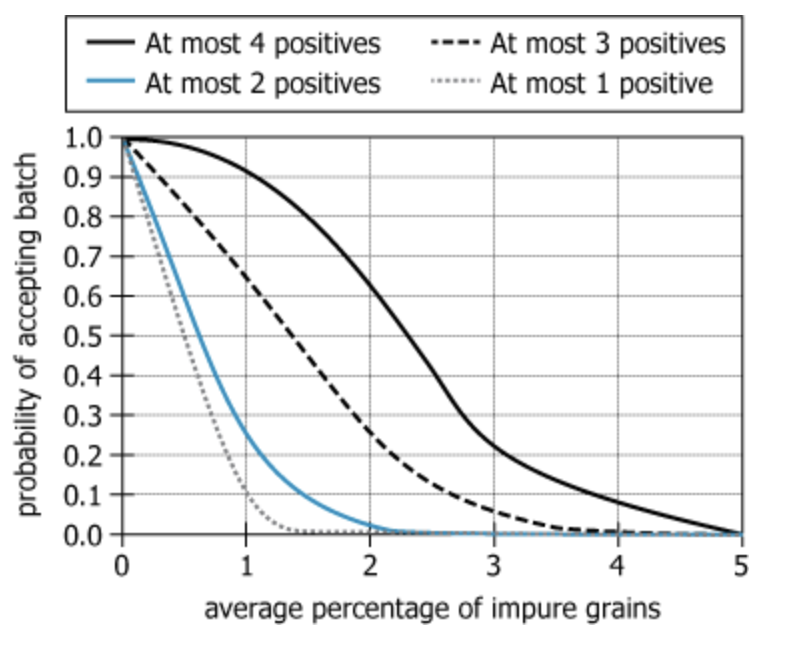
Before deciding whether to accept a batch of grain, agricultural-import inspectors in a certain country test five samples from the batch. The graph shows the probabilities that a batch will be accepted based on the average (arithmetic mean) percentage of impure grains found in the samples. The four curves represent how the probabilities of acceptance vary given four different standards for the maximum acceptable number of samples that test positive (are found to contain one or more impure grains). If all five samples test positive, the batch will not be accepted.
Select from the drop-down menus the options that create the statement that most accurately reflects the information provided in the graph.
Owning the Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Testing procedure | "agricultural-import inspectors in a certain country test five samples from the batch" | Inspectors take 5 samples from each grain batch |
| Decision purpose | "Before deciding whether to accept a batch of grain" | Tests determine if the batch passes import standards |
| Graph content | "the graph shows the probabilities that a batch will be accepted based on the average (arithmetic mean) percentage of impure grains found in the samples" | Chart displays how average impurity relates to acceptance likelihood |
| Standards for acceptance | "The four curves represent how the probabilities of acceptance vary given four different standards for the maximum acceptable number of samples that test positive (are found to contain one or more impure grains)" | 4 standards show how acceptance probability changes depending on allowed positive samples |
| Positive sample definition | "Positive: sample that contains one or more impure grains" | Any sample containing at least one impure grain is called 'positive' |
| Rejection rule | "If all five samples test positive, the batch will not be accepted" | Batches with 5/5 positives always get rejected |
Table 2: Chart Analysis
| Chart Component | Description | Interpretation |
|---|---|---|
| Chart type | Line chart, 4 curves | Each curve = a different acceptance rule |
| X-axis | Average % of impure grains (0% to 5%) | The mean impurity measured in the 5 tested samples |
| Y-axis | Probability batch is accepted (0.0 to 1.0) | Chance a batch is approved, given its average impurity |
| Acceptance standards | Curves for: at most 4 positives (solid), 3 (dashed), 2 (blue solid), 1 (dotted) | Stricter curves (allowed positives lower) drop faster |
| Curve trend | All curves start at 1.0 and decrease as impurity increases | More impurity means lower acceptance chance |
| Curve separation | Vertical gaps largest between curves at ~1%-2% impurity | Probability differences among standards greatest in this range |
| End behavior | Curves approach 0 as impurity nears 5% | Nearly all batches are rejected at high impurity |
Key Insights
The table and chart together show that as the average impurity increases, probability of batch acceptance drops under all standards, but the effect is most pronounced for more restrictive rules (lower allowed positives). The biggest differences in acceptance probability between standards occur in the \(1\%-2\%\) impurity range. At both extremes (\(0\%\) and high impurity), all standards lead to the same outcome: full acceptance at zero impurity and near-certain rejection at high impurity.
Step-by-Step Solution
Question 1: Determining the Average Percentage of Impure Grains Corresponding to a 0.35 Probability Difference
Complete Statement:
For a batch for which the average percentage of impure grains in the samples is [BLANK 1] percent, the probability that the inspectors will accept the batch is approximately \(0.35\) less if the maximum acceptable number of positive samples is [BLANK 2] than if it is 4.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: average percentage of impure grains in the samples
- Meaning: This is the mean impurity percentage calculated from all tested samples in a batch.
- Relation to Chart: The x-axis shows percentage of impure grains; we are looking for a specific x-value.
- Important Implications: Finding the correct impurity percentage is crucial for the comparison.
- Statement Breakdown 2:
- Key Phrase: probability that the inspectors will accept the batch
- Meaning: The likelihood (from 0 to 1) that a batch meets the acceptance standard.
- Relation to Chart: The y-axis displays probability; we must compare vertical gaps between curves.
- Important Implications: A change in acceptance criteria changes this probability.
What is needed: The specific impurity percentage (x-value) where the gap between the 'at most 4 positives' curve and another standard's curve is about \(0.35\).
Solution:
- Condensed Solution Implementation:
Examine the graph and estimate, for each impurity percentage labeled, the vertical difference between the probability for 'at most 4 positives' and lower acceptance standards. - Necessary Data points:
At \(2\%\) impurity: Probability of acceptance for 'at most 4 positives' is about \(0.65\). For 'at most 3 positives', it's about \(0.30\).- Calculations Estimations:
\(0.65\) (at most 4) - \(0.30\) (at most 3) = \(0.35\) probability difference. - Comparison to Answer Choices:
At \(2\%\), the difference between the two standards is closest to \(0.35\); at other impurity percentages the difference is either too large or too small.
- Calculations Estimations:
FINAL ANSWER Blank 1: 2
Question 2: Determining Which Maximum Acceptable Number of Positive Samples Gives a 0.35 Probability Difference
Complete Statement:
For a batch for which the average percentage of impure grains in the samples is 2 percent, the probability that the inspectors will accept the batch is approximately \(0.35\) less if the maximum acceptable number of positive samples is [BLANK 2] than if it is 4.
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: maximum acceptable number of positive samples is [BLANK 2] than if it is 4
- Meaning: We are comparing a stricter standard (allowing fewer positives) with the 'at most 4 positives' standard.
- Relation to Chart: We look for the curve that is \(0.35\) below the 'at most 4 positives' curve at \(2\%\) impurity.
What is needed: Which standard (at most 1, 2, or 3 positives) results in a probability of acceptance about \(0.35\) less than the standard allowing at most 4 positives at \(2\%\) impurity.
Solution:
- Condensed Solution Implementation:
On the chart at \(2\%\) impurity, check the probability difference between 'at most 4 positives' and each stricter criterion. - Necessary Data points:
'At most 4 positives': probability ≈ \(0.65\); 'at most 3 positives': ≈ \(0.30\).- Calculations Estimations:
\(0.65 - 0.30 = 0.35\). - Comparison to Answer Choices:
The only standard with a probability about \(0.35\) less than 'at most 4' at \(2\%\) impurity is 'at most 3 positives'.
- Calculations Estimations:
FINAL ANSWER Blank 2: 3
Summary
To get a probability difference of about \(0.35\) between acceptance standards for 5 samples, the impurity percentage is \(2\%\). At this percentage, moving from allowing at most 4 positive samples to at most 3 reduces the probability of acceptance by around \(0.35\).
Question Independence Analysis
The questions are linked: you must first find at what impurity percentage the specific probability difference occurs (blank 1), then determine which acceptance standard causes this (blank 2).