At the end of last semester, all 33 students (11 from each of 3 sections) of a particular course were...
GMAT Graphics Interpretation : (GI) Questions
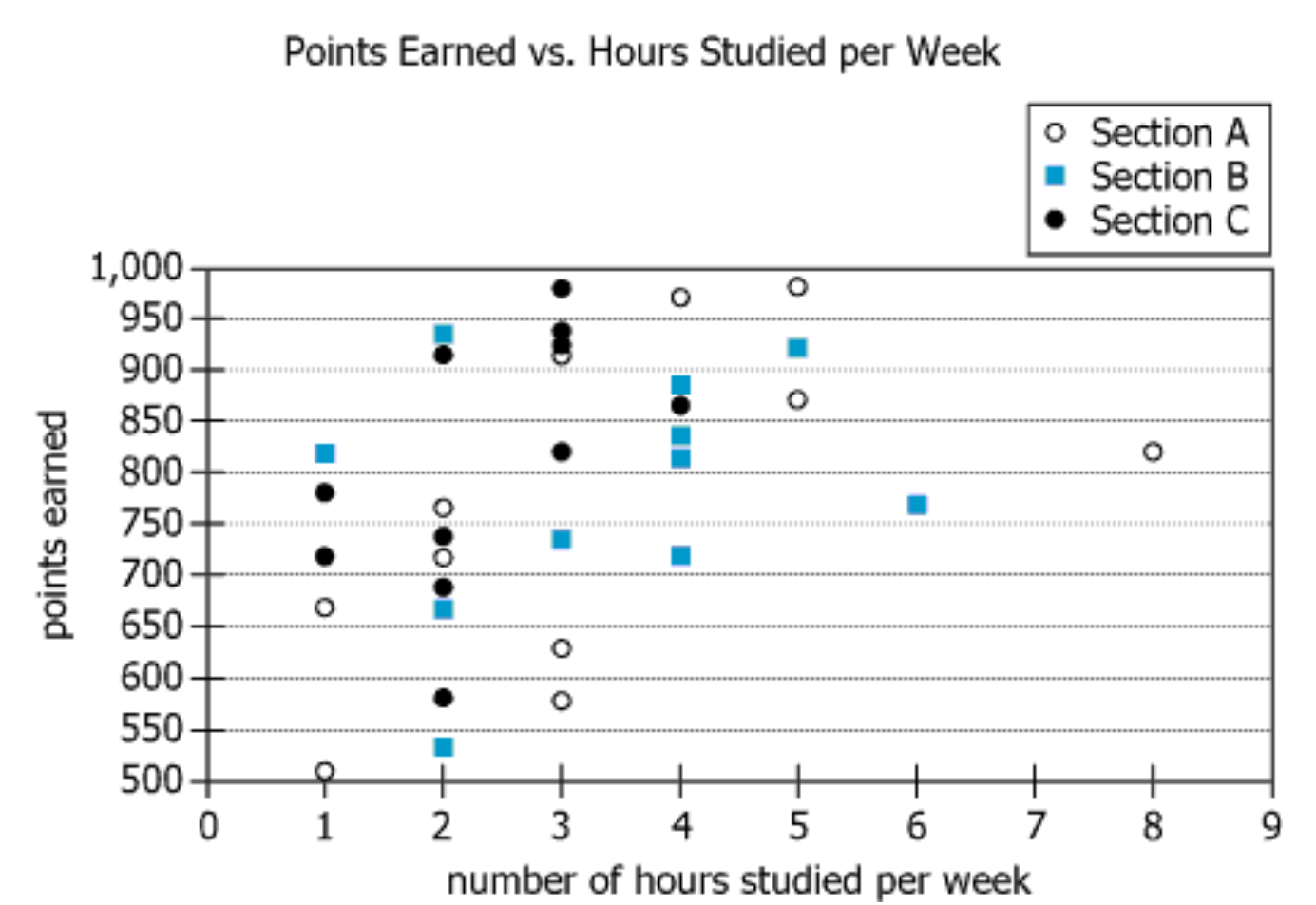
At the end of last semester, all 33 students (11 from each of 3 sections) of a particular course were asked how many hours per week they spent studying for the course. This data was combined with the number of points earned by each student in the course. This information is presented in the graph.
Grades in the course were calculated using a 20-point scale. To compute the grade, the number of points earned in the course was divided by 50 and then rounded up to the next whole number.
Use the drop-down menus to complete each statement so that it is consistent with the information provided.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Study Population | "all 33 students (11 from each of 3 sections) of a particular course" | There are 33 students total, split equally into three sections (A, B, C), each with 11 students. |
| Data Collected | "asked how many hours per week they spent studying for the course" | Each student self-reported the number of hours per week they studied for this course. |
| Combined With | "data was combined with the number of points earned by each student in the course" | The dataset includes, for every student, both their self-reported study hours and their actual points earned in the course. |
| Presentation | "This information is presented in the graph" | The summary of the students' study hours and earned points is depicted visually in a graph. |
| Grading Scale | "Grades in the course were calculated using a 20-point scale" | The course uses a 20-point grading rubric. |
| Grade Calculation | "number of points earned ... divided by 50 and then rounded up to ... whole number" | Grade = \(\mathrm{(points\ earned) ÷ 50}\), rounded up to the nearest whole number, so 751 points is grade 16. |
Table 2: Chart Analysis
| Chart Component | What's Shown | What This Tells Us |
|---|---|---|
| Graph Type | Scatter plot with 3 section marker types (A: open circles, B: filled squares, C: filled circles) | Each point on the plot represents a student; section membership is visually coded. |
| X-axis | Hours studied per week \(\mathrm{(0–9)}\) | Students reported anywhere from 0 up to around 9 hours of study weekly. |
| Y-axis | Points earned in course \(\mathrm{(500–1000)}\) | Students' performance varied from about 500 up to just under 1000 points (potentially out of 1000). |
| Number of Data Points | Section A (9), Section B (10), Section C (11) | Displayed points do not perfectly match the stated 11 students per section; some section data may be missing or miscounted. |
| Data Distribution | Clusters mostly between \(\mathrm{1–6\ hours}\) (x-axis), points spread across the y-axis | Most students studied 1–6 hours per week, but their scores covered most of the grade range. |
| Pattern/Trend | No clear linear pattern; scores vary widely for similar study hours | There is no strong visible correlation between study hours per week and points earned; high and low performers in all study bands. |
Key Insights
- There is no strong or consistent correlation between hours studied and points earned—students with similar study hours can have very different scores.
- Students who studied both low and moderate hours achieved a wide range of scores, indicating that study hours alone do not explain performance.
- Most students reported studying between 1 and 6 hours per week; few students were at the extremes.
- The points earned span a broad range \(\mathrm{(500\ to\ 1000)}\), which under the grading formula means actual grades from \(\mathrm{10\ to\ 20}\), covering the full possible grade spectrum.
Step-by-Step Solution
Question 1: Finding the Median Study Hours
Complete Statement:
The median reported time spent studying for all students in the course was ______ hours per week.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: median reported time
- Meaning: The value in the middle when all students' study hours are ordered from least to greatest.
- Relation to Chart: We must gather the study hours for all 33 students, sort them, and find the center value.
- Important Implications: Since 33 is an odd number, the median is the 17th value in the ordered list.
Statement Breakdown 2:
- Key Phrase: all students in the course
- Meaning: Includes every student from all three sections.
- Relation to Chart: Every data point on the chart, regardless of symbol, must be counted.
- Important Implications: No separation by section; we use the entire group for this median.
What is needed: What is the 17th smallest study hour value (the median) among all students?
Solution:
- Condensed Solution Implementation:
List all the reported study hours in order and locate the 17th one. - Necessary Data points:
Amounts of students who reported each possible study hour (e.g., how many reported 1 hour, 2 hours, etc.). - Calculations Estimations:
After counting, the cumulative total reaches 16 at 3 hours and 24 at 4 hours, so the 17th student is in the group who reported 3 hours. - Comparison to Answer Choices:
If the provided answers include 3, that's correct based on the ordering.
FINAL ANSWER Blank 1: 3
Question 2: Section with the Smallest Average Study Hours
Complete Statement:
Section ______ had the smallest average (arithmetic mean) reported time spent studying per week.
Breaking Down the Statement
Statement Breakdown 1:
- Key Phrase: smallest average (arithmetic mean)
- Meaning: The lowest value obtained by adding all study hours in a section and dividing by that section's number of students.
- Relation to Chart: Group the data by section and calculate averages for each.
Statement Breakdown 2:
- Key Phrase: reported time spent studying per week
- Meaning: Each student's numerical response appearing as their data point on the x-axis.
- Relation to Chart: The value for each student's position along the x-axis.
What is needed: Which section (A, B, or C) has the lowest average study hours?
Solution:
- Condensed Solution Implementation:
Sum all study hours for each section, then divide by 11 (students per section), and compare results. - Necessary Data points:
Section A: total ≈ 53 hours; Section B: total ≈ 46 hours; Section C: total ≈ 28 hours. - Calculations Estimations:
Averages: A ≈ 4.8, B ≈ 4.2, C ≈ 2.5; Section C is clearly the smallest. - Comparison to Answer Choices:
If one of the choices is Section C, it's the correct selection.
FINAL ANSWER Blank 2: C
Summary
To answer, we determined the median among all 33 study hour reports by finding the 17th value in order (which is 3), and calculated averages by section to discover Section C had the lowest (about 2.5 hours per week).
Question Independence Analysis
Blank 1 requires considering all students jointly for the median, while Blank 2 is about comparing averages by section. Each can be solved independently of the other.