A particular manufacturing company has exactly two manufacturing plants–Plants A and B. A consultant, using data about the company's past...
GMAT Graphics Interpretation : (GI) Questions
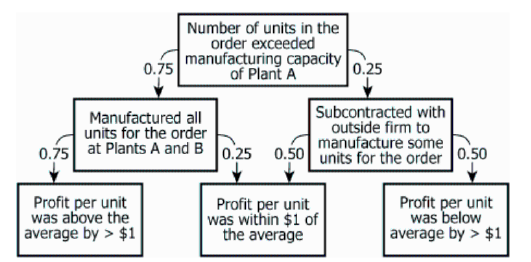
A particular manufacturing company has exactly two manufacturing plants–Plants A and B. A consultant, using data about the company's past performance and a particular model, calculated the probability of various outcomes when the company has promised to manufacture an order consisting of a greater number of units than could be produced only at the main plant, Plant A. Those probabilities are shown in the chart.
Select from each drop-down menu the opfon that creates the statement that most accurately reflects the information given.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Company Structure | has exactly two manufacturing plants–Plants A and B | The company has only 2 manufacturing facilities |
| Main Plant | the main plant, Plant A | Plant A is the primary plant; Plant B is auxiliary |
| Order Context | an order consisting of a greater number of units than could be produced only at Plant A | Analysis is for large orders exceeding Plant A's capacity |
| Probability Calculation Basis | using data about the company's past performance and a particular model | Past data and modeling are used for probability estimates |
| Probability Display | calculated the probability of various outcomes ... shown in the chart | The chart summarizes all relevant probabilities |
Table 2: Chart Analysis
| Chart Component | What's Shown | Interpretation |
|---|---|---|
| Root Node | Order exceeds Plant A's capacity | All scenarios are for large orders |
| First Branch | 75% In-house (A+B), 25% Subcontract | Company mostly prefers in-house production |
| In-house Outcomes | 75% profit >$1 above average, 25% within $1 of avg. | In-house yields mainly high profits, moderate profit also possible |
| Subcontract Outcomes | 50% profit >$1 above, 50% profit >$1 below average | Subcontracting leads to only extreme profit outcomes |
Key Insights
- Only in-house production can result in profits within $1 of average (probability 18.75%).
- Subcontracting leads to extreme results: equally likely to be much better or much worse than average (no middle outcomes).
- For large orders, the company overwhelmingly prefers in-house (75% of cases), favoring more consistent and better profits.
Step-by-Step Solution
Question 1: Manufacturing Path Probability
Complete Statement:
The chart indicates that, for an order selected at random from those consisting of more units than could be produced by Plant A, the probability that the company's profit per unit on that order was within $1 of the average is equal to the sum of [BLANK 1] and...
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: order selected at random from those consisting of more units than could be produced by Plant A
- Meaning: The focus is only on orders larger than Plant A's capacity.
- Relation to Chart: All probabilities in the tree apply only to these large orders – it's the root of the decision tree.
- Important Implications: Probabilities shown later in the tree are conditional on this starting point.
- Statement Breakdown 2:
- Key Phrase: probability that the company's profit per unit on that order was within $1 of the average
- Meaning: Looking for orders that achieved a 'within $1 of average' profit outcome.
- Relation to Chart: Must consider each possible branch that can result in this outcome.
- Important Implications: We must add up these probabilities.
- What is needed: The probability from the manufacturing branch that results in a profit within $1 of average.
Solution:
- Condensed Solution Implementation:
Multiply probability of manufacturing (0.75) by probability of 'within $1' given manufacturing (0.25). - Necessary Data points:
Probability for manufacturing: 0.75; Probability for 'within $1' given manufacturing: 0.25. - Calculations Estimations:
\(0.75 \times 0.25 = 0.1875\) - Comparison to Answer Choices:
0.1875 matches an answer choice, so this is the correct value for BLANK 1.
FINAL ANSWER Blank 1: 0.1875
Question 2: Subcontracting Path Probability
Complete Statement:
...and [BLANK 2]
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: and [BLANK 2]
- Meaning: This is the other portion of the probability sum, referring to the subcontracting path.
- Relation to Chart: Represents probability of getting profit within $1 of average in the subcontracting branch.
- What is needed: The probability from the subcontracting branch that results in a profit within $1 of average.
Solution:
- Condensed Solution Implementation:
Multiply probability of subcontracting (0.25) by probability of 'within $1' given subcontracting (0.50). - Necessary Data points:
Probability for subcontracting: 0.25; Probability for 'within $1' given subcontracting: 0.50. - Calculations Estimations:
\(0.25 \times 0.50 = 0.125\) - Comparison to Answer Choices:
0.125 matches an answer choice for BLANK 2.
FINAL ANSWER Blank 2: 0.125
Summary
To find the required probability, add the probabilities of both manufacturing and subcontracting branches leading to 'profit within $1 of average'. The total is \(0.1875 + 0.125 = 0.3125\).
Question Independence Analysis
BLANK 1 and BLANK 2 correspond to distinct branches (manufacturing and subcontracting, respectively), but both are required to find the total probability as specified by the question. Thus, they are related and dependent in the context of solving the problem.