A certain product must be subjected to (and pass) a sequence of various combinations of 5 tests (Tests A through...
GMAT Graphics Interpretation : (GI) Questions
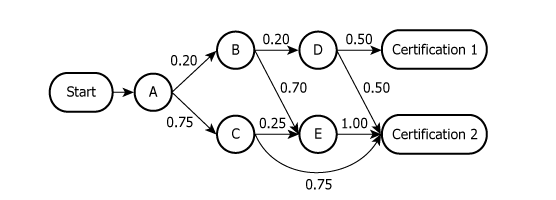
A certain product must be subjected to (and pass) a sequence of various combinations of 5 tests (Tests A through E) before it may receive one of two certifications (Certification 1 or Certification 2). The diagram shows how products proceed through these tests, along with the probability of proceeding from each test to the next test or certification. For instance, the diagram shows that an item subjected to Test A has a 0.20 probability of passing Test A and being subjected to Test B next, a 0.75 probability of passing Test A and being subjected to Test C next, and a 0.05 probability of failing Test A. The probability that an item receives either of the two certifications is exactly 0.93.
Based on the information provided, select from each drop-down menu the option that creates the most accurate statement.
Owning The Dataset
Table 1: Text Analysis
| Text Component | Literal Content | Simple Interpretation |
|---|---|---|
| Product testing process | A certain product must be subjected to (and pass) a sequence of various combinations of 5 tests (Tests A through E)... | Products are tested in various orders using Tests A–E |
| Certification outcomes | ...before it may receive one of two certifications (Certification 1 or Certification 2). | There are two possible certifications products can earn |
| Probability explained | The diagram shows ... probability of proceeding from each test to the next test or certification. | Each testing step has specific probabilities attached |
| Test A example | ...Test A has a \(0.20\) probability of passing ... to Test B next, \(0.75\) probability ... to Test C next, and \(0.05\) ... fail... | From Test A: \(20%\) to B, \(75%\) to C, \(5%\) fail the process |
| Overall certification rate | The probability ... receives either of the two certifications is exactly \(0.93\). | \(93%\) of products succeed; \(7%\) fail overall |
Table 2: Chart Analysis
| Chart Element | Description/Values | Interpretation |
|---|---|---|
| Flow type | Directed flow diagram with nodes (Start, A–E, Certifications) and probability-labeled arrows | Sequence of tests with probabilistic branches |
| Nodes | Start, A, B, C, D, E, Certification 1, Certification 2 | Each letter is a test; endpoints are certifications |
| Key probability paths | \(\mathrm{A \rightarrow B: 0.20}\); \(\mathrm{A \rightarrow C: 0.75}\); \(\mathrm{A \text{ fail}: 0.05}\); \(\mathrm{B \rightarrow D: 0.20}\); \(\mathrm{C \rightarrow E: 0.25}\); \(\mathrm{C \rightarrow \text{Certification 2}: 0.75}\); \(\mathrm{D \rightarrow \text{Certification 1}: 0.50}\); \(\mathrm{E \rightarrow \text{Certification 1}: 0.70}\); \(\mathrm{E \rightarrow \text{Certification 2}: 1.00}\) | Outlines all possible test transitions and their likelihoods |
| Shortest certification | \(\mathrm{A \rightarrow C \rightarrow \text{Certification 2}}\) | Most direct/high probability route to Certification 2 |
| Multiple routes | Various paths (including through nodes B, D, E) | Products have redundancy in reaching certification |
Key Insights
The dataset mapping reveals most products traverse from Test A to C, then directly to Certification 2: this is both the shortest and highest-probability route (\(0.75 \times 0.75 = 0.5625\), or \(56.25%\)). The system is designed so the vast majority (\(93%\)) eventually succeed, with products able to take multiple routes to certification, minimizing overall failure. The flow diagram's redundant paths help ensure quality assurance by requiring products to potentially pass several tests before certifying. Node E functions as a crucial convergence point, providing access to both certifications from different upstream pathways.
Step-by-Step Solution
Question 1: Probability of Receiving Certification 1
Complete Statement:
To the nearest hundredth, the probability that a randomly selected product subjected to Test A will receive Certification 1 is [BLANK].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: randomly selected product subjected to Test A
- Meaning: We are considering only those products that enter Test A.
- Relation to Chart: Test A is the starting node after 'Start' in the diagram.
- Important Implications: Every probability calculation should use Test A as the reference start.
- Statement Breakdown 2:
- Key Phrase: will receive Certification 1
- Meaning: We are interested only in products that reach Certification 1.
- Relation to Chart: Certification 1 is one of the outcome nodes in the flow diagram.
- Important Implications: We must find all possible paths from Test A to Certification 1 and sum their probabilities.
What is needed: Calculate the probability that a product starting at Test A ends at Certification 1 along any valid path.
Solution:
- Condensed Solution Implementation:
Identify all possible distinct paths from Test A to Certification 1 in the diagram. For each path, multiply the transition probabilities along the path; then sum the probabilities for all such paths. - Necessary Data points:
\(\mathrm{A \text{ to } B} = 0.20\); \(\mathrm{B \text{ to } D} = 0.20\); \(\mathrm{D \text{ to Certification 1}} = 0.50\). - Calculations Estimations:
Path: \(\mathrm{A \rightarrow B \rightarrow D \rightarrow \text{Certification 1}} = 0.20 \times 0.20 \times 0.50 = 0.02\); No other path from A leads to Certification 1. - Comparison to Answer Choices:
\(0.02\) matches one of the answer choices.
FINAL ANSWER Blank 1: 0.02
Question 2: Probability of Receiving Certification 2
Complete Statement:
To the nearest hundredth, the probability that a randomly selected product subjected to Test A will receive Certification 2 is [BLANK].
Breaking Down the Statement
- Statement Breakdown 1:
- Key Phrase: randomly selected product subjected to Test A
- Meaning: We are again focusing on all products starting at Test A.
- Relation to Chart: Same starting population as in question 1.
- Statement Breakdown 2:
- Key Phrase: will receive Certification 2
- Meaning: Find the probability of reaching Certification 2.
- Relation to Chart: Certification 2 is the other terminal output node.
What is needed: Calculate the probability that a product starting at Test A finishes at Certification 2.
Solution:
- Condensed Solution Implementation:
Since \(93%\) of all products are certified and only \(2%\) reach Certification 1, the remainder to \(93%\) are those reaching Certification 2. - Necessary Data points:
Total certification probability is \(0.93\). Probability of Certification 1 is \(0.02\). Failure from Test A is \(0.05\) (but already excluded in the total certification rate). - Calculations Estimations:
Certification 2 probability = \(0.93 - 0.02 = 0.91\). - Comparison to Answer Choices:
\(0.91\) matches one of the available choices.
FINAL ANSWER Blank 2: 0.91
Summary
By tracing the unique path from Test A to Certification 1 and then using the overall certification rate, we efficiently found the requested probabilities. The probability of Certification 1 is low (\(0.02\)), and the remainder of the \(93%\) total certification goes to Certification 2 (\(0.91\)).
Question Independence Analysis
The two questions are mathematically dependent—they must sum (when combined with all failure probabilities from Test A) to the overall total, so knowing one immediately gives the other.